题目内容
已知定义在R上的函数f(x)和g(x)满足g(x)≠0,f′(x)•g(x)<f(x)•g′(x),f(x)=ax•g(x),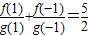 .令
.令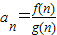 ,则使数列{an}的前n项和Sn超过
,则使数列{an}的前n项和Sn超过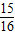 的最小自然数n的值为 .
的最小自然数n的值为 .
【答案】分析:分别令x等于1和x等于-1代入①得到两个关系式,把两个关系式代入②得到关于a的方程,求出方程的解即可得到a的值,根据f′(x)•g(x)<f(x)•g′(x)可知 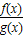 =ax 是减函数,对求得的a进行取舍,求出数列{an}的通项公式,进而求得其前n项和Sn,解不等式Sn≤
=ax 是减函数,对求得的a进行取舍,求出数列{an}的通项公式,进而求得其前n项和Sn,解不等式Sn≤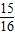 ,即可求得结果.
,即可求得结果.
解答:解:令x=1,得到f(1)=a•g(1);令x=-1,f(-1)=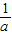 •g(-1).
•g(-1).
代入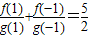 可得 a+
可得 a+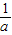 =
= ,化简得2a2-5a+2=0,即(2a-1)(a-2)=0,解得a=2或a=
,化简得2a2-5a+2=0,即(2a-1)(a-2)=0,解得a=2或a= .
.
∵f′(x)•g(x)<f(x)•g′(x),∴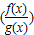 ′<0,
′<0,
从而可得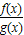 =ax 是减函数,故a=
=ax 是减函数,故a= .
.
∴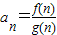 =
=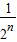 ,Sn=
,Sn=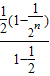 =1-
=1-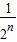 .
.
再由 1-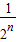 >
>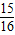 解得 n>4,故 n的最小值为5,
解得 n>4,故 n的最小值为5,
故答案为 5.
点评:题考查学生会利用有理数指数幂公式化简求值,利用导数研究函数的单调性,等比数列求和等知识,综合性强,根据已知求出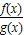 =ax 的单调性是解题的关键,考查运算能力和应用知识分析解决问题的能力,属中档题.
=ax 的单调性是解题的关键,考查运算能力和应用知识分析解决问题的能力,属中档题.
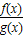 =ax 是减函数,对求得的a进行取舍,求出数列{an}的通项公式,进而求得其前n项和Sn,解不等式Sn≤
=ax 是减函数,对求得的a进行取舍,求出数列{an}的通项公式,进而求得其前n项和Sn,解不等式Sn≤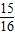 ,即可求得结果.
,即可求得结果.解答:解:令x=1,得到f(1)=a•g(1);令x=-1,f(-1)=
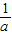 •g(-1).
•g(-1).代入
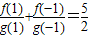 可得 a+
可得 a+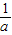 =
= ,化简得2a2-5a+2=0,即(2a-1)(a-2)=0,解得a=2或a=
,化简得2a2-5a+2=0,即(2a-1)(a-2)=0,解得a=2或a= .
.∵f′(x)•g(x)<f(x)•g′(x),∴
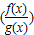 ′<0,
′<0,从而可得
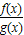 =ax 是减函数,故a=
=ax 是减函数,故a= .
.∴
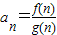 =
=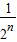 ,Sn=
,Sn=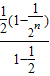 =1-
=1-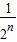 .
.再由 1-
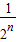 >
>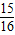 解得 n>4,故 n的最小值为5,
解得 n>4,故 n的最小值为5,故答案为 5.
点评:题考查学生会利用有理数指数幂公式化简求值,利用导数研究函数的单调性,等比数列求和等知识,综合性强,根据已知求出
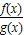 =ax 的单调性是解题的关键,考查运算能力和应用知识分析解决问题的能力,属中档题.
=ax 的单调性是解题的关键,考查运算能力和应用知识分析解决问题的能力,属中档题. 
练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |