题目内容
已知sin| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
分析:先根据sin
-cos
=-
求出sinα的值,再由角α范围确定tanα的值,从而得到答案.
| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
解答:解:∵sin
-cos
=-
∴1-2sin
cos
=1-sinα=
∴sinα=
∵450°<α<540°,∴tanα=
故答案为:
| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
∴1-2sin
| α |
| 2 |
| α |
| 2 |
| 1 |
| 5 |
∴sinα=
| 4 |
| 5 |
∵450°<α<540°,∴tanα=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题主要考查同角三角函数的基本关系.考查基础知识的基本运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: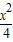
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.