题目内容
抛物线y=x2上的一动点M到直线l：x-y-1=0距离的最小值是
- A.
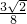
- B.
- C.
- D.
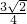
A
分析：（法一）对y=x2求导可求与直线x-y-1=0平行且与抛物线y=x2相切的切线方程，然后利用两平行线的距离公司可得所求的最小距离d
（法二）设抛物线上的任意一点M（m，m2），由点到直线的距离公司可求M到直线x-y-1=0的距离d=
=
=
，由二次函数的性质可求M到直线x-y-1=0的最小距离
解答：（法一）对y=x2求导可得y′=2x
令y′=2x=1可得
∴与直线x-y-1=0平行且与抛物线y=x2相切的切点（
，
），切线方程为y-
即x-y
由两平行线的距离公司可得所求的最小距离d=
=
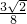
（法二）设抛物线上的任意一点M（m，m2）
M到直线x-y-1=0的距离d===
由二次函数的性质可知，当m=时，最小距离d=
=
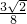
故选A
点评：本题考查直线的抛物线的位置关系的应用，解题时要注意公式的灵活运用，抛物线的基本性质和点到线的距离公式的应用，考查综合运用能力
分析：（法一）对y=x2求导可求与直线x-y-1=0平行且与抛物线y=x2相切的切线方程，然后利用两平行线的距离公司可得所求的最小距离d
（法二）设抛物线上的任意一点M（m，m2），由点到直线的距离公司可求M到直线x-y-1=0的距离d=
==，由二次函数的性质可求M到直线x-y-1=0的最小距离解答：（法一）对y=x2求导可得y′=2x
令y′=2x=1可得
∴与直线x-y-1=0平行且与抛物线y=x2相切的切点（
，），切线方程为y-即x-y由两平行线的距离公司可得所求的最小距离d=
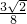
=（法二）设抛物线上的任意一点M（m，m2）
M到直线x-y-1=0的距离d=
==由二次函数的性质可知，当m=
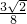
时，最小距离d==故选A
点评：本题考查直线的抛物线的位置关系的应用，解题时要注意公式的灵活运用，抛物线的基本性质和点到线的距离公式的应用，考查综合运用能力
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
已知抛物线y=x2上有一定点A（-1，1）和两动点P、Q，当PA⊥PQ时，点Q的横坐标取值范围是（ ）
| A、（-∞，-3] | B、[1，+∞） | C、[-3，1] | D、（-∞，-3]∪[1，+∞） |