题目内容

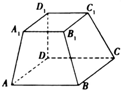精英家教网已知四棱台ABCD-A1B1C1D1（如图）中，底面ABCD是正方形，且DD1⊥底面ABCD，AB=2A1B1=2DD1=2a．
（1）求异面直线AB1与DD1所成角的余弦值；
（2）试在平面ADD1A1中确定一个点F，使得FB1⊥平面BCC1B1．
分析：（1）以D为原点，DA、DC、DD1所在的直线为x，y，z轴，建立空间直角坐标系，写出要用的点的坐标，写出两条直线所对应的方向向量，求出异面直线所成的角．
（2）设出点F的坐标，根据线面FB1⊥平面BCC1B1得到两对向量的数量积等于0，得到关于所设的未知量的方程，解方程即可．
解答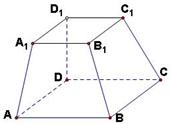：精英家教网解：以D为原点，DA、DC、DD1所在的直线为x，y，z轴，建立空间直角坐标系，
则D（0，0，0），A（2a，0，0），B1（a，a，a），D1（0，0，a），B（2a，2a，0），C（0，2a，0），C1（0，a，a）
（1）∵
AB1
=（-a，a，a），
DD1
=（0，0，a），
∴cos＜
AB
1，
DD1
＞=
AB
1•
DD
1
AB
1•
DD1
=
a2
3a2
a2
=
3
3
，
即直线AB1与DD1所成角的余角的余弦值为
3
3

（2）设F（x，0，z），
∵
BB
=（-a，-a，a），
BC
=（-2a，0，0），
FB1
=（a-x，a1，a-z），
由FB1⊥平面BCC1B1得
FB1
•
BB1
=0
FB1
•
BC
=0
即
-a(a-x)-a2+a(a-z)=0
-2a(a-x)=0
得
x=a
z=0

∴F（a，0，0），即F为DA的中点．
点评：本题考查用向量语言来表示线面的平行和垂直关系，本题解题的关键是建立坐标系，把理论的推导变化成了数字的运算，降低了题目的难度．
练习册系列答案
相关题目
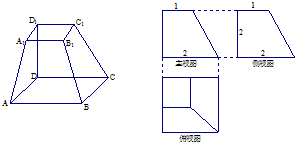已知四棱台ABCD-A1B1C1D1的三视图如图所示，
（1）求证：BB1∥平面D1AC；
（2）求证：平面D1AC⊥平面B1BDD1；
（3）求此四棱台ABCD-A1B1C1D1的体积．
（2012•武昌区模拟）如图，已知四棱台ABCD-A1B1C1D1的侧棱A1A垂直于底面ABCD．底面ABCD是边长为2的正方形，四边形A1B1C1D1是边长为1的正方形，DD1=2．
（I）求证：平面A1ACC1⊥平面B1BDD1；
（II）求侧棱DD1与底面ABCD所成的角；
（III）求四棱台ABCD-A1B1C1D1的体积．
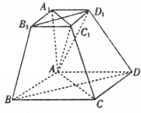（2012•安徽模拟）如图，已知四棱台ABCD-A1B1C1D1的侧棱A1A垂直于底面AB-CD，底面ABCD是边长为2的正方形，四边形A1B1C1D1是边长为1的正方形，DD1=2．
（1）求证：平面A1ACC1丄平面B1BDD1
（2）求四棱锥A-CDD1C1的体积．
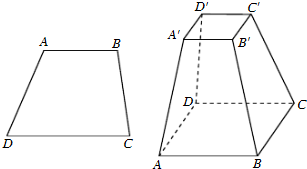（必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
设OE=x，∵△OAB∽△ODC，∴
x
x+h
=
a
b
，即x=
ah
b-a
．
∴S梯形ABCD=S△ODC-S△OAB=
1
2
b（x+h）-
1
2
ax=
1
2
（b-a）x+
1
2
bh=
1
2
（a+b）h．
方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
设梯形AMNB的高为x，MN=y，
x
h
=
y-a
b-a
⇒y=a+
b-a
h
x，∴S梯形ABCD=
∫
h
0
（a+
b-a
h
x）dx=（ax+
b-a
2h
x2）
|
h
0
=ah+
b-a
2h
•h2=
1
2
（a+b）h．
再解下面的问题：
已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
1
3
×底面积×高）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网