题目内容
(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分。已知数列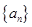 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为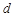 ,
,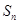 为其前
为其前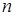 项和,且满足
项和,且满足
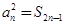 ,
,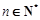 .数列
.数列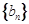 满足
满足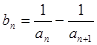 ,
,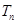 为数列
为数列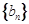 的前n项和.
的前n项和.
(1)求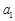 、
、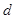 和
和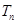 ;
;
(2)若对任意的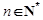 ,不等式
,不等式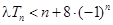 恒成立,求实数
恒成立,求实数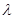 的取值范围
的取值范围
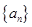 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为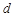 ,
,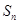 为其前
为其前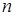 项和,且满足
项和,且满足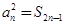 ,
,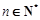 .数列
.数列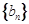 满足
满足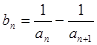 ,
,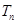 为数列
为数列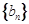 的前n项和.
的前n项和.(1)求
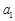 、
、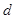 和
和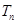 ;
;(2)若对任意的
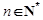 ,不等式
,不等式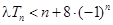 恒成立,求实数
恒成立,求实数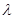 的取值范围
的取值范围(1)  ;
; ;
;

(2)
 ;
; ;
;

(2)

等差数列的通项公式及应用是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,这是近几年新课标高考对数列考查的一个亮点,也是一种趋势.随着新课标实施的深入,高考关注的重点为等差、等比数列的通项公式,错位相减法、裂项相消法等求数列的前n项的和等等
解:
(1) .……………………………. 1分
.……………………………. 1分
 ,
, ,当
,当 时,
时, 不满足条件,舍去.因此
不满足条件,舍去.因此 .……………………………. 4分
.……………………………. 4分
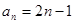 ,
, ,
, 。
。
……………………………. 6分
(2)当 为偶数时,
为偶数时, ,
,
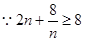 ,当
,当 时等号成立,
时等号成立, 最小值为
最小值为 ,
,
因此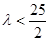 。 ……………………………. 9分
。 ……………………………. 9分
当 为奇数时,
为奇数时, ,
,
 在
在 时单调递增,
时单调递增, 时
时 的最小值为
的最小值为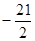 ,
,
 。 ……………………………. 12分
。 ……………………………. 12分
综上, 。 ……………………………. 14分
。 ……………………………. 14分
解:
(1)
 .……………………………. 1分
.……………………………. 1分 ,
, ,当
,当 时,
时, 不满足条件,舍去.因此
不满足条件,舍去.因此 .……………………………. 4分
.……………………………. 4分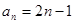 ,
, ,
, 。
。……………………………. 6分
(2)当
 为偶数时,
为偶数时, ,
,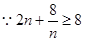 ,当
,当 时等号成立,
时等号成立, 最小值为
最小值为 ,
,因此
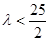 。 ……………………………. 9分
。 ……………………………. 9分当
 为奇数时,
为奇数时, ,
, 在
在 时单调递增,
时单调递增, 时
时 的最小值为
的最小值为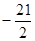 ,
, 。 ……………………………. 12分
。 ……………………………. 12分综上,
 。 ……………………………. 14分
。 ……………………………. 14分
练习册系列答案
相关题目
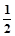 ,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。
,且前n项和Sn满足:Sn=n2an,求a2,a3,a4,猜想{an}的通项公式,并加以证明。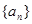 ,满足
,满足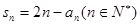
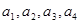 ,并猜想通项公式
,并猜想通项公式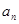 。
。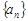 满足:
满足: ;
;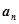 ;(2).令
;(2).令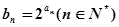 ,求数列
,求数列 的前n项积
的前n项积 。
。 的前
的前 项和为
项和为 ,已知
,已知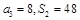 ,数列
,数列 满足
满足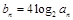 .
. ,使得
,使得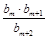 是数列
是数列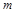 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 个等式为 .
个等式为 .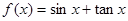 ,项数为29的等差数列
,项数为29的等差数列 满足
满足 ,且公差
,且公差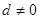 ,若
,若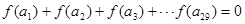 ,
, 时,
时, 的值 ( )
的值 ( ) 中,前
中,前 项和
项和 ,则
,则 ▲ .
▲ . 中,
中, +
+ +
+ =12,那么
=12,那么 ( )
( )