题目内容
A∈平面α．AB=5，AC=2
，若AB与α所成角正弦值为0.8，AC与α成450角，则BC距离的范围（ ）
| 2 |
分析：作BD⊥α，垂足为D，作CE⊥α，垂足为E，连接AE，AD，DE，过C作CF⊥BD，垂足为F，根据AB与α所成角正弦值为0.8，AC与α成450角，
求得AE，CE，BD，AD，设∠DAE=θ，分BC在平面α的同侧和异侧两种情况列出BC关于θ的函数式，根据0≤θ≤π，求出BC的求值范围．
求得AE，CE，BD，AD，设∠DAE=θ，分BC在平面α的同侧和异侧两种情况列出BC关于θ的函数式，根据0≤θ≤π，求出BC的求值范围．
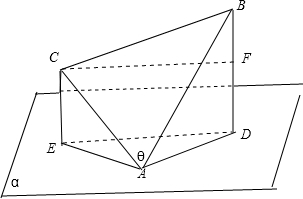
解答：解：当B、C在平面α的同侧时如图作BD⊥α，垂足为D，作CE⊥α，垂足为E，连接AE，AD，DE，
过C作CF⊥BD，垂足为F，
则AD、AE分别为AB、AC在α内的射影，∴∠BAD，∠CAE分别为AB、AC与平面α所成的角，
∵AB与α所成角正弦值为0.8，AC与α成450角，
∴AE=CE=2，BD=4，AD=3，
设∠DAE=θ，BF=4-2
∴BC=
=
=
，
∵0≤θ≤π，∴
≤BC≤
当B、C在平面α的异侧时，BF=4+2=6，
则BC=
=
，
∵0≤θ≤π，∴
≤BC≤
．
故选D．
过C作CF⊥BD，垂足为F，
则AD、AE分别为AB、AC在α内的射影，∴∠BAD，∠CAE分别为AB、AC与平面α所成的角，
∵AB与α所成角正弦值为0.8，AC与α成450角，
∴AE=CE=2，BD=4，AD=3，
设∠DAE=θ，BF=4-2
∴BC=
| CF2+BF2 |
| 4+9+4-2×2×3×cosθ |
| 17-12cosθ |
∵0≤θ≤π，∴
| 5 |
| 29 |
当B、C在平面α的异侧时，BF=4+2=6，
则BC=
| CF2+BF2 |
| 36+9+4-2×2×3×cosθ |
∵0≤θ≤π，∴
| 37 |
| 61 |
故选D．
点评：本题考查了直线与平面所成的角，考查了学生的作图能力与空间想象能力，体现了分类讨论思想与数形结合思想，正确的作出图形是解答本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
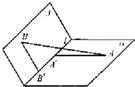如图，α和β为平面，α∩β=l，A∈α，B∈β，AB=5，A，B在棱l上的射影分别为A′，B′，AA′=3，BB′=2．若二面角α-l-β的大小为
，
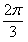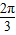，求：
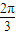，求：
，求：