题目内容
已知奇函数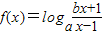 ,(a>0,且a≠1)
,(a>0,且a≠1)(Ⅰ)求b的值;
(Ⅱ)对于x∈[2,4]
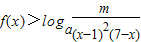 恒成立,求m的取值范围;
恒成立,求m的取值范围;(Ⅲ)当n≥4,且n∈N*时,试比较af(2)+f(3)+…+f(n)与2n-2的大小.
【答案】分析:(I)根据奇函数的定义g(x)=-g(-x)列出关于b的等式,由函数的奇偶性定义求出b的值;
(II)分当a>1和当0<a<1两种情况讨论,利用分离参数法,结合导数在最大值、最小值问题中的应用来解m的取值范围.
(Ⅲ)先得出: ,再分情况讨论:当n=2时,
,再分情况讨论:当n=2时, ,2n-2=2,∴af(2)+f(3)++f(n)>2n-2;当n=3时,
,2n-2=2,∴af(2)+f(3)++f(n)>2n-2;当n=3时, ,2n-2=6,∴af(2)+f(3)++f(n)=2n-2;当n≥4时,
,2n-2=6,∴af(2)+f(3)++f(n)=2n-2;当n≥4时, 2n-2进行证明即可.
2n-2进行证明即可.
解答:解:(Ⅰ)由 ,
,

∴ 恒成立,b2=1,b=±1经检验b=1
恒成立,b2=1,b=±1经检验b=1
(Ⅱ)由x∈[2,4]时, 恒成立,
恒成立,
①当a>1时
∴ 对x∈[2,4]恒成立
对x∈[2,4]恒成立
∴0<m<(x+1)(x-1)(7-x)在x∈[2,4]恒成立
设g(x)=(x+1)(x-1)(7-x),x∈[2,4]
则g(x)=-x3+7x2+x-7
∴当x∈[2,4]时,g'(x)>0
∴y=g(x)在区间[2,4]上是增函数,g(x)min=g(2)=15
∴0<m<15
②当0<a<1时
由x∈[2,4]时, 恒成立,
恒成立,
∴ 对x∈[2,4]恒成立
对x∈[2,4]恒成立
∴m>(x+1)(x-1)(7-x)在x∈[2,4]恒成立
设g(x)=(x+1)(x-1)(7-x),x∈[2,4]
由①可知y=g(x)在区间[2,4]上是增函数,g(x)max=g(4)=45
∴m>45
综上,当a>1时,0<m<15;
当0<a<1时,m>45
(Ⅲ)∵ =
=
∴
当n=2时, ,2n-2=2,∴af(2)+f(3)++f(n)>2n-2
,2n-2=2,∴af(2)+f(3)++f(n)>2n-2
当n=3时, ,2n-2=6,∴af(2)+f(3)++f(n)=2n-2
,2n-2=6,∴af(2)+f(3)++f(n)=2n-2
当n≥4时, 2n-2
2n-2
下面证明:当n≥4时, 2n-2
2n-2
当n≥4时,2n-2=Cn+Cn1+Cn2++Cnn-1+Cnn-2=Cn1+Cn2++Cnn-1
∴当n≥4时, 2n-2
2n-2
 n≥4时,
n≥4时, ,即
,即 2n-2
2n-2
∴当n≥4时, 2n-2.
2n-2.
点评:本题是函数性质的综合题,本小题主要考查函数奇偶性的性质、函数奇偶性的应用、不等式的解法、导数在最大值、最小值问题中的应用等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
(II)分当a>1和当0<a<1两种情况讨论,利用分离参数法,结合导数在最大值、最小值问题中的应用来解m的取值范围.
(Ⅲ)先得出:
 ,再分情况讨论:当n=2时,
,再分情况讨论:当n=2时, ,2n-2=2,∴af(2)+f(3)++f(n)>2n-2;当n=3时,
,2n-2=2,∴af(2)+f(3)++f(n)>2n-2;当n=3时, ,2n-2=6,∴af(2)+f(3)++f(n)=2n-2;当n≥4时,
,2n-2=6,∴af(2)+f(3)++f(n)=2n-2;当n≥4时, 2n-2进行证明即可.
2n-2进行证明即可.解答:解:(Ⅰ)由
 ,
,

∴
 恒成立,b2=1,b=±1经检验b=1
恒成立,b2=1,b=±1经检验b=1(Ⅱ)由x∈[2,4]时,
 恒成立,
恒成立,①当a>1时
∴
 对x∈[2,4]恒成立
对x∈[2,4]恒成立∴0<m<(x+1)(x-1)(7-x)在x∈[2,4]恒成立
设g(x)=(x+1)(x-1)(7-x),x∈[2,4]
则g(x)=-x3+7x2+x-7

∴当x∈[2,4]时,g'(x)>0
∴y=g(x)在区间[2,4]上是增函数,g(x)min=g(2)=15
∴0<m<15
②当0<a<1时
由x∈[2,4]时,
 恒成立,
恒成立,∴
 对x∈[2,4]恒成立
对x∈[2,4]恒成立∴m>(x+1)(x-1)(7-x)在x∈[2,4]恒成立
设g(x)=(x+1)(x-1)(7-x),x∈[2,4]
由①可知y=g(x)在区间[2,4]上是增函数,g(x)max=g(4)=45
∴m>45
综上,当a>1时,0<m<15;
当0<a<1时,m>45
(Ⅲ)∵
 =
=
∴

当n=2时,
 ,2n-2=2,∴af(2)+f(3)++f(n)>2n-2
,2n-2=2,∴af(2)+f(3)++f(n)>2n-2当n=3时,
 ,2n-2=6,∴af(2)+f(3)++f(n)=2n-2
,2n-2=6,∴af(2)+f(3)++f(n)=2n-2当n≥4时,
 2n-2
2n-2下面证明:当n≥4时,
 2n-2
2n-2当n≥4时,2n-2=Cn+Cn1+Cn2++Cnn-1+Cnn-2=Cn1+Cn2++Cnn-1

∴当n≥4时,
 2n-2
2n-2 n≥4时,
n≥4时, ,即
,即 2n-2
2n-2∴当n≥4时,
 2n-2.
2n-2.点评:本题是函数性质的综合题,本小题主要考查函数奇偶性的性质、函数奇偶性的应用、不等式的解法、导数在最大值、最小值问题中的应用等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
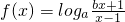 ,(a>0,且a≠1)
,(a>0,且a≠1)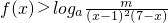 恒成立,求m的取值范围;
恒成立,求m的取值范围;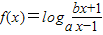 ,(a>0,且a≠1)
,(a>0,且a≠1)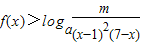 恒成立,求m的取值范围;
恒成立,求m的取值范围;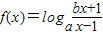 ,(a>0,且a≠1)
,(a>0,且a≠1) 恒成立,求m的取值范围;
恒成立,求m的取值范围; ,(a>0,且a≠1)
,(a>0,且a≠1)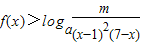 恒成立,求m的取值范围;
恒成立,求m的取值范围;