题目内容
设函数 的定义域为
的定义域为
 ,值域为
,值域为 ,若
,若 的最小值为
的最小值为 ,则实数a的值为( )
,则实数a的值为( )
A. | B. 或 或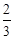 | C.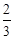 | D.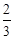 或 或 |
D
解析试题分析:①若1≤m<n,则f(x)=-logax,
∵f(x)的值域为[0,1],∴f(m)=0,f(n)=1,解得m=1,n=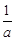 ,
,
又∵n-m的最小值为  ,∴
,∴ -1≥
-1≥ ,及0<a<1,当等号成立时,解得a=
,及0<a<1,当等号成立时,解得a= .
.
②若0<m<n<1,则f(x)=logax,
∵f(x)的值域为[0,1],∴f(m)=1,f(n)=0,解得m=a,n=1,又∵n-m的最小值为  ,∴1-a≥
,∴1-a≥ ,
,
及0<a<1,当等号成立时,解得a=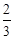 .
.
③若0<m<1<n时,不满足题意,故选D。
考点:本题主要考查对数函数的性质,绝对值的概念。
点评:中档题,注意运用分类讨论思想,确定m,n,的可能情况。本题易错,忽视不同情况的讨论。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知函数 若有
若有 则
则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
设二次函数 的值域为
的值域为 ,则
,则 的最小值为
的最小值为
A. | B.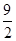 | C. | D. |
已知 ,
, =( )
=( )
A. | B.0 | C.1 | D.2 |
已知 且方程
且方程 恰有
恰有 个不同的实数根,则实数
个不同的实数根,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设 ,且
,且 ,则
,则
A. | B.10 | C.20 | D.100 |
不等式 的解集为
的解集为 ,那么 ( )
,那么 ( )
A. | B. | C. | D. |
设 ( )
( )
| A.0 | B.1 | C.2 | D.3 |