题目内容
已知函数f(x)=lnx-ax.
(1)求f(x)的单调区间;
(2)f(x)=0在[1,e2]上有解,求a的取值范围.
解:(Ⅰ)定义域为(0,+∞)
当a≤0时,f′(x)>0恒成立,f(x)的单调递增区间为(0,+∞)
当a>0时,令
令
故f(x)的单调递增区间为 ,单调递减区间为
,单调递减区间为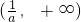
(Ⅱ)lnx-ax=0在x∈[1,e2]上有解
故 在x∈[1,e2]上有解
在x∈[1,e2]上有解
令

令g′(x)=0得x=e
∴
∴
分析:(1)对函数f(x)求导,当导数f'(x)大于0时可求单调增区间,当导数f'(x)小于0时可求单调减区间.
(2)f(x)=0在[1,e2]上有解即 在x∈[1,e2]上有解,转化为求函数
在x∈[1,e2]上有解,转化为求函数 在[1,e2]上的取值范围.
在[1,e2]上的取值范围.
点评:本题主要考查通过求函数的导数来确定函数增减区间的问题.

当a≤0时,f′(x)>0恒成立,f(x)的单调递增区间为(0,+∞)
当a>0时,令

令

故f(x)的单调递增区间为
 ,单调递减区间为
,单调递减区间为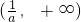
(Ⅱ)lnx-ax=0在x∈[1,e2]上有解
故
 在x∈[1,e2]上有解
在x∈[1,e2]上有解令


令g′(x)=0得x=e

∴

∴

分析:(1)对函数f(x)求导,当导数f'(x)大于0时可求单调增区间,当导数f'(x)小于0时可求单调减区间.
(2)f(x)=0在[1,e2]上有解即
 在x∈[1,e2]上有解,转化为求函数
在x∈[1,e2]上有解,转化为求函数 在[1,e2]上的取值范围.
在[1,e2]上的取值范围.点评:本题主要考查通过求函数的导数来确定函数增减区间的问题.

练习册系列答案
相关题目