题目内容
定义在R上的函数f(x)满足f(x+1)=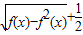 ,f(1)=1,已知an=f2(n)-f(n),则数列{an}的前40项和 .
,f(1)=1,已知an=f2(n)-f(n),则数列{an}的前40项和 .
【答案】分析:根据题中函数关系式化简整理,得到[f2(x+1)-f(x+1)]-[f2(x)-f(x)]=- ,结合题意算出an+1-an=-
,结合题意算出an+1-an=- ,从而得到{an}构成公差d=-
,从而得到{an}构成公差d=- 的等差数列,由f(1)=1算出a1=0,得到通项公式an=
的等差数列,由f(1)=1算出a1=0,得到通项公式an= (1-n),最后利用等差数列的前n项和公式即可算出数列{an}的前40项和.
(1-n),最后利用等差数列的前n项和公式即可算出数列{an}的前40项和.
解答:解:∵f(x+1)=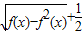 ,
,
∴f(x+1)- =
=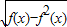 ,
,
两边平方,得[f(x+1)- ]2=f(x)-f2(x)
]2=f(x)-f2(x)
化简得[f2(x+1)-f(x+1)]-[f2(x)-f(x)]=-
∵an=f2(n)-f(n),可得an+1=f2(n+1)-f(n+1),
∴an+1-an=[f2(n+1)-f(n+1)]-[f2(n)-f(n)]=- ,
,
可得{an}构成公差d=- 的等差数列
的等差数列
∵f(1)=1,得a1=f2(1)-f(1)=0
∴{an}的通项公式为an=a1+(n-1)d= (1-n)
(1-n)
因此,数列{an}的前40项和为S40=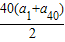 =20×(-
=20×(-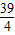 )=-195
)=-195
故答案为:-195
点评:本题给出函数关系式,在已知数列an=f2(n)-f(n)的情况下求数列的前n项和.着重考查了函数式的配方整理、数列递推关系,等差数列的通项公式与求和公式等知识,属于中档题.
 ,结合题意算出an+1-an=-
,结合题意算出an+1-an=- ,从而得到{an}构成公差d=-
,从而得到{an}构成公差d=- 的等差数列,由f(1)=1算出a1=0,得到通项公式an=
的等差数列,由f(1)=1算出a1=0,得到通项公式an= (1-n),最后利用等差数列的前n项和公式即可算出数列{an}的前40项和.
(1-n),最后利用等差数列的前n项和公式即可算出数列{an}的前40项和.解答:解:∵f(x+1)=
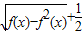 ,
,∴f(x+1)-
 =
=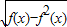 ,
,两边平方,得[f(x+1)-
 ]2=f(x)-f2(x)
]2=f(x)-f2(x)化简得[f2(x+1)-f(x+1)]-[f2(x)-f(x)]=-

∵an=f2(n)-f(n),可得an+1=f2(n+1)-f(n+1),
∴an+1-an=[f2(n+1)-f(n+1)]-[f2(n)-f(n)]=-
 ,
,可得{an}构成公差d=-
 的等差数列
的等差数列∵f(1)=1,得a1=f2(1)-f(1)=0
∴{an}的通项公式为an=a1+(n-1)d=
 (1-n)
(1-n)因此,数列{an}的前40项和为S40=
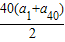 =20×(-
=20×(-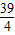 )=-195
)=-195故答案为:-195
点评:本题给出函数关系式,在已知数列an=f2(n)-f(n)的情况下求数列的前n项和.着重考查了函数式的配方整理、数列递推关系,等差数列的通项公式与求和公式等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目