题目内容
设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H(1)求抛物线C的方程;
(2)设M是抛物线C上一点,E(0,4),延长ME、MF分别交抛物线C于点A、B,若A、B、H三点共线,求点M的坐标.

【答案】分析:(1)由抛物线的定义,结合P到焦点的距离为4建立关于p的方程,解出p=2即得抛物线C方程;
(2)设M(t,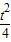 ),由点斜式可写出直线MF、ME的方程,分别与抛物线方程联立可解出点B、点A的坐标,根据A、B、H三点共线,得kAH=kBH,由此可解出t值;
),由点斜式可写出直线MF、ME的方程,分别与抛物线方程联立可解出点B、点A的坐标,根据A、B、H三点共线,得kAH=kBH,由此可解出t值;
解答:解:(1)由题意得抛物线C的准线l方程为:y=-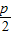 ,
,
因为抛物线C上的点P(m,3)到焦点的距离是4,得3-(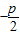 )=4,解得P=2
)=4,解得P=2
所以抛物线方程为:x2=4y.
(2)设M(t,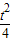 ),又直线过点F(0,1),则直线MF方程为y-1=
),又直线过点F(0,1),则直线MF方程为y-1=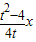 ,
,
过点E(0,4)直线ME方程为y-4=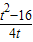 x,
x,
由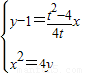 ,得B(
,得B(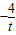 ,
,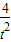 ),
),
由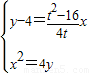 ,得A(-
,得A(-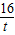 ,
,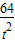 ),
),
则kAH=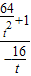 =
=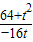 ,kBH=
,kBH=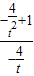 =
=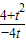 ,
,
∵A、B、H三点共线,∴kAH=kBH,即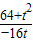 =
=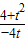 解得t=±4,
解得t=±4,
∴M点的坐标为(±4,4).
点评:本题主要考查了抛物线的简单性质,考查抛物线的标准方程,考查直线与抛物线的位置关系,属于难题.
(2)设M(t,
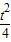 ),由点斜式可写出直线MF、ME的方程,分别与抛物线方程联立可解出点B、点A的坐标,根据A、B、H三点共线,得kAH=kBH,由此可解出t值;
),由点斜式可写出直线MF、ME的方程,分别与抛物线方程联立可解出点B、点A的坐标,根据A、B、H三点共线,得kAH=kBH,由此可解出t值;解答:解:(1)由题意得抛物线C的准线l方程为:y=-
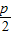 ,
,因为抛物线C上的点P(m,3)到焦点的距离是4,得3-(
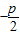 )=4,解得P=2
)=4,解得P=2所以抛物线方程为:x2=4y.
(2)设M(t,
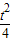 ),又直线过点F(0,1),则直线MF方程为y-1=
),又直线过点F(0,1),则直线MF方程为y-1=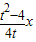 ,
,过点E(0,4)直线ME方程为y-4=
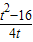 x,
x,由
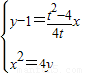 ,得B(
,得B(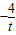 ,
,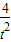 ),
),由
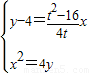 ,得A(-
,得A(-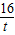 ,
,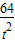 ),
),则kAH=
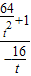 =
=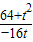 ,kBH=
,kBH=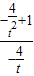 =
=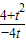 ,
,∵A、B、H三点共线,∴kAH=kBH,即
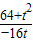 =
=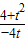 解得t=±4,
解得t=±4,∴M点的坐标为(±4,4).
点评:本题主要考查了抛物线的简单性质,考查抛物线的标准方程,考查直线与抛物线的位置关系,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
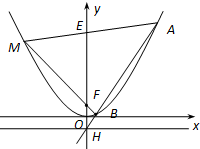 设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H
设抛物线C:x2=2py(p>0),F为焦点,抛物线C上一点P(m,3)到焦点的距离是4,抛物线C的准线l与y轴的交点为H