题目内容
已知数列{an}的前n项和为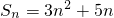 ,数列{bn}中b1=8,bn=64bn+1.
,数列{bn}中b1=8,bn=64bn+1.
(1)求{bn}的通项bn;
(2)证明{an}是等差数列;
(3)是否存在常数a、b,使得对一切正整数n都有an=logabn+b成立.若存在,求出a、b的值;若不存在,说明理由.
解:(1)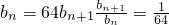 ,
,
∴ ,
,
∴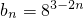 …(3分)
…(3分)
(2)当n≥2时:
又n=1时:a1=S1=8=6×1+2
∴an=6n+2.…(6分)
∴an-an-1=6n+2-6(n-1)-2=6
∴{an}是等差数列 …(7分)
(3)假设存在这样的a、b,使得对一切自然数n都有an=logabn+b成立,则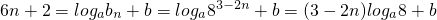 =
= .
.
令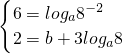 …(10分)
…(10分)
 ,
,
∴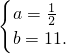
∴存在这样的数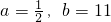 .…(12分)
.…(12分)
分析:(1)由数列{bn}中b1=8,bn=64bn+1.能求出公式 ,由此能求出数列{bn}的通项公式
,由此能求出数列{bn}的通项公式
(2)由数列{an}的前n项和为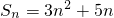 ,能求出an=6n+2,由此能够证明{an}是等差数列.
,能求出an=6n+2,由此能够证明{an}是等差数列.
(3)假设存在这样的a、b,使得对一切自然数n都有an=logabn+b成立,则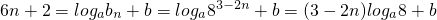 ,由此入手,能够求出a、b的值.
,由此入手,能够求出a、b的值.
点评:本试题主要考查等比数列和等差数列的通项公式的求解以及数列的综合运用.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
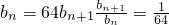 ,
,∴
 ,
,∴
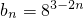 …(3分)
…(3分)(2)当n≥2时:

又n=1时:a1=S1=8=6×1+2
∴an=6n+2.…(6分)
∴an-an-1=6n+2-6(n-1)-2=6
∴{an}是等差数列 …(7分)
(3)假设存在这样的a、b,使得对一切自然数n都有an=logabn+b成立,则
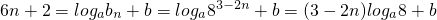 =
= .
.令
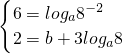 …(10分)
…(10分) ,
,∴
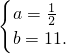
∴存在这样的数
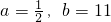 .…(12分)
.…(12分)分析:(1)由数列{bn}中b1=8,bn=64bn+1.能求出公式
 ,由此能求出数列{bn}的通项公式
,由此能求出数列{bn}的通项公式(2)由数列{an}的前n项和为
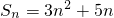 ,能求出an=6n+2,由此能够证明{an}是等差数列.
,能求出an=6n+2,由此能够证明{an}是等差数列.(3)假设存在这样的a、b,使得对一切自然数n都有an=logabn+b成立,则
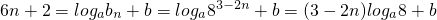 ,由此入手,能够求出a、b的值.
,由此入手,能够求出a、b的值.点评:本试题主要考查等比数列和等差数列的通项公式的求解以及数列的综合运用.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |