题目内容
已知双曲线
-
=1(a＞0，b＞0)的焦点坐标是F1(-c,0)和F2(c,0),P（x0,y0）是双曲线上的任一点，求证:|PF1|=|a+ex0|,|PF2|=|a-ex0|，其中e是双曲线的离心率.
证明:双曲线-=1的两焦点为F1(-c,0)、F2(c,0)，相应的准线方程分别是x=-
和x=
.?
∵双曲线上任一点到焦点的距离与它到相应准线的距离的比等于这个双曲线的离心率，
∴
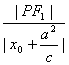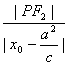=e，
=e.
化简得|PF1|=|a+ex0|,|PF2|=|a-ex0|.
温馨提示:|PF1|、|PF2|都是双曲线上的点到其焦点的距离，通常称作焦半径.|PF1|=|a+ex0|,|PF2|=|a-ex0|称作焦半径公式.
练习册系列答案
相关题目
=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,
=1(a＞0,b＞0)的离心率e∈［
,2］，令双曲线两条渐近线构成的角中，以实轴为角平分线的角为θ,则θ的取值范围是( )
］ B.［
］
］ D.［
,π］
=1(a＞0，b＞0)的右焦点为F，若过F且倾斜角为60°的直线与双曲线有且只有一个交点，则双曲线的离心率是( )
B．
C．4 D．2
=1(a＞0,b＞0)的一条渐近线为y=kx(k＞0),离心率e=
k,则双曲线方程为( )
=1 B.
=1
=1 D.
=1
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
(O为原点),则两条渐近线的夹角为( )