题目内容
已知单调递增的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2和a4的等差中项，
（1）求数列{an}的通项公式an；
（2）令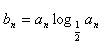
，Sn=b1+b2+…+bn，求使Sn+n·2n+1＞50成立的最小的正整数n。
（1）求数列{an}的通项公式an；
（2）令
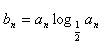，Sn=b1+b2+…+bn，求使Sn+n·2n+1＞50成立的最小的正整数n。解：（1）设{an}的公比为q，由已知，得
，
∴
；
（2）
，
设
，…………①
则
， ………②
①－②得
，
∴
，
故
，
∴
，
，
∴满足不等式的最小的正整数n为5。
，∴
； （2）
，设
，…………① 则
， ………②①－②得
，∴
，故
，∴
，，∴满足不等式的最小的正整数n为5。
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目