题目内容
已知函数f(x)=kx3-x2+x-5在R上单调递增,则实数k的取值范围是
- A.
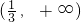
- B.
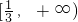
- C.
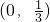
- D.
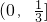
B
分析:因为在函数的增区间上导数大于0,所以若函数f(x)=kx3-x2+x-5在R上单调递增,它的导数大于等于0恒成立,就转变为一元二次不等式恒成立问题,在利用一元二次不等式的解的情况求k的范围.
解答:f′(x)=3kx2-2x+1,
∵f(x)=kx3-x2+x-5在R上单调递增,
∴f′(x)>0在R上恒成立
即3kx2-2x+1≥0恒成立.
当k=0时,不等式变为-x+1>0,不满足条件,
当k>0时,只需△=4-12k≤0即可
解得,k≥
故选B
点评:本题主要考查利用导数求函数的单调区间,以及根据一元二次不等式解的情况求参数范围.
分析:因为在函数的增区间上导数大于0,所以若函数f(x)=kx3-x2+x-5在R上单调递增,它的导数大于等于0恒成立,就转变为一元二次不等式恒成立问题,在利用一元二次不等式的解的情况求k的范围.
解答:f′(x)=3kx2-2x+1,
∵f(x)=kx3-x2+x-5在R上单调递增,
∴f′(x)>0在R上恒成立
即3kx2-2x+1≥0恒成立.
当k=0时,不等式变为-x+1>0,不满足条件,
当k>0时,只需△=4-12k≤0即可
解得,k≥

故选B
点评:本题主要考查利用导数求函数的单调区间,以及根据一元二次不等式解的情况求参数范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目