题目内容
把函数y=lnx-2的图象按向量a=(-1,2)平移得到函数y=f(x)的图象.(1)若x>0,证明:f(x)>![]() ;
;
(2)若不等式![]() x2≤f(x2)+m2-2bm-3时x∈[-1,1]都恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2bm-3时x∈[-1,1]都恒成立,求实数m的取值范围.
证:(1)由题设得f(x)=ln(x+1),
令g(x)=f(x)-![]() =ln(x+1)-
=ln(x+1)-![]() 则g′(x)=
则g′(x)=![]() >0.
>0.
∴g(x)在(0,+∞)上是增函数,又g(x)在x=0处连续,
∴g(x)>g(0)=0,即f(x)>![]() .
.
(2)原不等式等价于![]() x2-f(x)2≤m2-2bm-3,
x2-f(x)2≤m2-2bm-3,
令h(x)=![]() x2-f(x2)=
x2-f(x2)=![]() x2-ln(1+x2),则h′(x)=x-
x2-ln(1+x2),则h′(x)=x-![]() ,
,
令h′(x)=0得 x=0,x=1,x=-1,列表如下:
x | -1 | (-1,0) | 0 | (0,1) | 1 |
h′(x) | 0 | + | 0 | - | 0 |
| 极小值 | ↗ | 极大值0 | ↙ | 极小值 |
∴当x∈[-1,1]时,h(x)max=0,∴m2-2bm-3≥0.
令Q(b)=-2mb+m2-3,则Q(1)=m2-2m-3≥0,Q(-1)=m2+2m-3≥0.
得m≤-3或m≥3.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
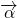 =(-1,2)平移得到函数y=f(x)的图象.
=(-1,2)平移得到函数y=f(x)的图象. ;
; x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.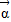 =(-1,2)平移得到函数y=f(x)的图象.
=(-1,2)平移得到函数y=f(x)的图象. ;
; x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.
x2≤f(x2)+m2-2bm-3对b∈[-1,1],x∈[-1,1]时恒成立,求实数m的取值范围.