题目内容
已知数列{an}满足:a1=1,an+1=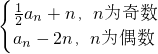
(1)求a2、a3、a4、a5;
(2)设bn=a2n-2,n∈N,求证{bn}是等比数列,并求其通项公式;
(3)在(2)条件下,求证数列{an}前100项中的所有偶数项的和S100<100.
解:(1) ;
;
(2)∵
= ,
,
又∵ ,
,
∴数列{bn}是等比数列,
且 ;
;
(3)由(2)得:
 (n=1,2,…,50)
(n=1,2,…,50)
∴ =99+
=99+ <100.
<100.
分析:(1)由数列{an}满足:a1=1,an+1=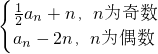 ,分别令n=2,3,4,5代入解出函数值即可;
,分别令n=2,3,4,5代入解出函数值即可;
(2)由于bn=a2n-2,要证明{bn}是等比数列,利用等比数列的定义即可得到,在利用等比数列的通项公式求出通项;
(3)在(2)条件下得: (n=1,2,…,50),由通项公式利用分组求和及等比数列的求和公式即可求得.
(n=1,2,…,50),由通项公式利用分组求和及等比数列的求和公式即可求得.
点评:此题考查了有数列的递推关系求前5项的数值,等比数列的定义及通项公式,分组求和及等比数列的求和公式.
 ;
;(2)∵

=
 ,
,又∵
 ,
,∴数列{bn}是等比数列,
且
 ;
;(3)由(2)得:
 (n=1,2,…,50)
(n=1,2,…,50)∴
 =99+
=99+ <100.
<100.分析:(1)由数列{an}满足:a1=1,an+1=
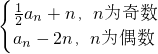 ,分别令n=2,3,4,5代入解出函数值即可;
,分别令n=2,3,4,5代入解出函数值即可;(2)由于bn=a2n-2,要证明{bn}是等比数列,利用等比数列的定义即可得到,在利用等比数列的通项公式求出通项;
(3)在(2)条件下得:
 (n=1,2,…,50),由通项公式利用分组求和及等比数列的求和公式即可求得.
(n=1,2,…,50),由通项公式利用分组求和及等比数列的求和公式即可求得.点评:此题考查了有数列的递推关系求前5项的数值,等比数列的定义及通项公式,分组求和及等比数列的求和公式.

练习册系列答案
相关题目