题目内容
给出如下两个命题:命题p:f(x)=
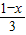 ,且|f(a)|<2
,且|f(a)|<2命题q:集合A={x|x2+(a+2)x+1=0},B={x|x>0},且A∩B=φ.
求实数a的取值范围,使命题p,q中至少有一个为真命题.
【答案】分析:依题意,可求得命题p:-5<a<7;命题q为:a>-4;依题意,命题p,q中至少有一个为真命题?①若p真q假或②若p假q真或③若p真q真,分别解之,最后取其并集即可.
解答:解:命题p中|f(a)|<2,即|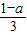 |<2,化简得,-5<a<7; …(2分)
|<2,化简得,-5<a<7; …(2分)
命题q中A∩B=φ,即方程x2+(a+2)x+1=0没有正实根,
则△=(a+2)2-4<0,解得-4<a<0;或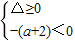 ,解得a≥0,
,解得a≥0,
∴命题q可化简为a>-4.…(5分)
①若p真q假,则-5<a≤-4,即a∈(-5,-4]; …(7分)
②若p假q真,则a≥7,即a∈[7,+∞]; …(9分)
③若p真q真,则-4<a<7,即a∈(-4,7).…(11分)(-5,-4]∪[7,+∞]∪(-4,7)=(-5,+∞).…(13分)
综上可知,当a∈(-5,+∞)时,命题p,q中至少有一个为真命题.…(14分)
点评:本题考查命题的真假判断与应用,着重考查等价转化思想与分类讨论思想的综合应用,求得命题p:-5<a<7与命题q:a>-4是关键,也是难点,属于难题.
解答:解:命题p中|f(a)|<2,即|
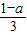 |<2,化简得,-5<a<7; …(2分)
|<2,化简得,-5<a<7; …(2分)命题q中A∩B=φ,即方程x2+(a+2)x+1=0没有正实根,
则△=(a+2)2-4<0,解得-4<a<0;或
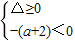 ,解得a≥0,
,解得a≥0,∴命题q可化简为a>-4.…(5分)
①若p真q假,则-5<a≤-4,即a∈(-5,-4]; …(7分)
②若p假q真,则a≥7,即a∈[7,+∞]; …(9分)
③若p真q真,则-4<a<7,即a∈(-4,7).…(11分)(-5,-4]∪[7,+∞]∪(-4,7)=(-5,+∞).…(13分)
综上可知,当a∈(-5,+∞)时,命题p,q中至少有一个为真命题.…(14分)
点评:本题考查命题的真假判断与应用,着重考查等价转化思想与分类讨论思想的综合应用,求得命题p:-5<a<7与命题q:a>-4是关键,也是难点,属于难题.

练习册系列答案
相关题目