题目内容
设点(a,b)在平面区域D={(a,b)||a|≤1,|b|≤1}中按均匀分布出现,则椭圆 (a>b>0)的离心率e<
(a>b>0)的离心率e< 的概率为 .
的概率为 .
【答案】分析:先计算平面区域D的面积,作为基本事件空间,再由椭圆离心率的范围计算椭圆a、b间的不等式,作为概率事件的约束条件,并画出其对应的平面区域,计算其面积,最后由几何概型概率计算公式计算概率即可
解答:解:如图 平面区域D为如图的正方形ABCD及其内部,其面积为S=2×2=4
平面区域D为如图的正方形ABCD及其内部,其面积为S=2×2=4
∵椭圆 (a>b>0)的离心率e<
(a>b>0)的离心率e< ,
,
∴ <
< ,即a<2b
,即a<2b
设事件A={椭圆 (a>b>0)的离心率e<
(a>b>0)的离心率e< }
}
则事件A对应的平面区域为 ,如图阴影部分,
,如图阴影部分,
面积为S(A)=1- -
- =
=
∴事件A发生的概率P(A)= =
= =
=
故答案为 .
.
点评:本题考查了二维几何概型的概率计算,椭圆的几何性质,准确的画出事件对应的平面区域是解决本题的关键
解答:解:如图
 平面区域D为如图的正方形ABCD及其内部,其面积为S=2×2=4
平面区域D为如图的正方形ABCD及其内部,其面积为S=2×2=4∵椭圆
 (a>b>0)的离心率e<
(a>b>0)的离心率e< ,
,∴
 <
< ,即a<2b
,即a<2b设事件A={椭圆
 (a>b>0)的离心率e<
(a>b>0)的离心率e< }
}则事件A对应的平面区域为
 ,如图阴影部分,
,如图阴影部分,面积为S(A)=1-
 -
- =
=
∴事件A发生的概率P(A)=
 =
= =
=
故答案为
 .
.点评:本题考查了二维几何概型的概率计算,椭圆的几何性质,准确的画出事件对应的平面区域是解决本题的关键

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
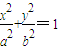 (a>b>0)的离心率e<
(a>b>0)的离心率e<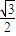 的概率为 .
的概率为 . (a>b>0)的离心率e<
(a>b>0)的离心率e< 的概率为 .
的概率为 .