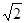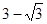题目内容
在△ 中,
中, 分别为内角
分别为内角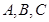 的对边,且
的对边,且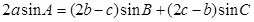 .
.
(1)求角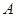 的大小;
的大小;
(2)若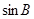 +
+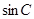 =
=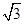 ,试判断△
,试判断△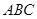 的形状.
的形状.
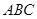 中,
中,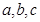 分别为内角
分别为内角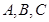 的对边,且
的对边,且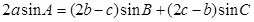 .
.(1)求角
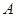 的大小;
的大小;(2)若
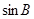 +
+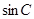 =
=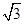 ,试判断△
,试判断△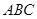 的形状.
的形状.解:(1)由2asin A=(2b-c)sin B+(2c-b)sin C,
得2a2=(2b-c)b+(2c-b)c,即bc=b2+c2-a2,
∴cos A=
 =
= ,∴A=60°. 5分
,∴A=60°. 5分(2)∵A+B+C=180°,∴B+C=180°-60°=120°.
由sin B+sin C=
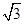 ,得sin B+sin(120°-B)=
,得sin B+sin(120°-B)=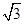 ,
,∴sin B+sin 120°cos B-cos 120°sin B=
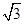 .
.∴
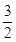 sin B+
sin B+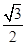 cos B=
cos B=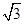 ,即sin(B+30°)=1. -----------9分
,即sin(B+30°)=1. -----------9分∵0°<B<120°,∴30°<B+30°<150°.
∴B+30°=90°,B=60°. ∴A=B=C=60°,△ABC为正三角形.
本试题主要考查了解三角形中正弦定理和余弦定理的运用。求解变和角,并定形的问题。

练习册系列答案
相关题目
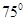 ,
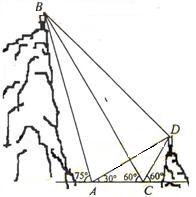
, ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为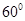 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,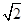
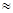 1.414,
1.414,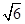
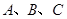 是
是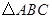 的三个内角,且满足
的三个内角,且满足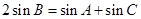 ,设
,设 的最大值为
的最大值为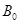 .
.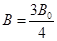 时,求
时,求 的值.
的值.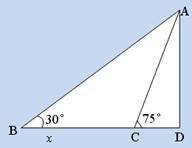
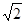 m
m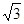 m
m ABC中,
ABC中,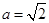 ,
, , 则角A=
, 则角A= 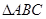 中,
中,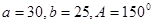 ,则
,则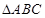 的三内角
的三内角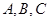 的对边边长分别为
的对边边长分别为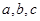 ,若
,若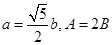 ,则
,则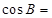
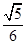
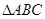 中,
中,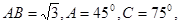 则BC =( )
则BC =( )