题目内容
例5:(1)lg(x-y)+lg(x+2y)=lg2+lgx+lgy求| x |
| y |
(2)
| lgx+lgy |
| lgx |
| lgx+lgy |
| lgy |
| [lg(x-y)]2 |
| lgx•lgy |
分析:(1)利用对数的运算法则将方程左右两边化为同底的一个对数,去掉对数符号,分子、分母同除以y2,解二次方程即可.
(2)通分得到两个式子的平方和为0,得到此两个数都为0,列出方程组求出x,y的值,代入log2(x•y)求出值.
(2)通分得到两个式子的平方和为0,得到此两个数都为0,列出方程组求出x,y的值,代入log2(x•y)求出值.
解答:解:(1)原方程变形为lg(x-y)(x+2y)=lg(2xy)
所以x2-xy-2y2=0
同除以y2得(
)2-
-2=0
解得
=2或
=-1(舍去)
(2)原方程同解于(lgx+lgy)2+lg(x-y)2=0
∴
∴
解得
∴log2(x•y)=log21=0
所以x2-xy-2y2=0
同除以y2得(
| x |
| y |
| x |
| y |
解得
| x |
| y |
| x |
| y |
(2)原方程同解于(lgx+lgy)2+lg(x-y)2=0
∴
|
∴
|
解得
|
∴log2(x•y)=log21=0
点评:本题考查对数的运算法则、考查二次方程的解法、考查两个数的平方和为0,两个数都是0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )y-3≥1,且y∈N*},C={(x,y)|x∈A,y∈B},D={1,2,3,4,5},从C到D的对应f:(x,y)→x+y,则f是否是从C到D的映射?
)y-3≥1,且y∈N*},C={(x,y)|x∈A,y∈B},D={1,2,3,4,5},从C到D的对应f:(x,y)→x+y,则f是否是从C到D的映射?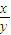 的值
的值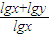 +
+ +
+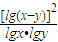 =0,求x,y及log2.
=0,求x,y及log2.