题目内容
 (2012•黄州区模拟)2012年春晚歌舞类节目成为春晚顶梁柱,尤其是不少创意组合都被网友称赞很有新意.王力宏和李云迪的钢琴PK,加上背景板的黑白键盘,更被网友称赞是行云流水的感觉.某网站从2012年1月23号到1月30做了持续一周的在线调查,共有n人参加调查,现将数据整理分组如题中表格所示.
(2012•黄州区模拟)2012年春晚歌舞类节目成为春晚顶梁柱,尤其是不少创意组合都被网友称赞很有新意.王力宏和李云迪的钢琴PK,加上背景板的黑白键盘,更被网友称赞是行云流水的感觉.某网站从2012年1月23号到1月30做了持续一周的在线调查,共有n人参加调查,现将数据整理分组如题中表格所示.| 序号 | 年龄分组 | 组中值mi | 频数(人数) | 频率(f) |
| 1 | [20,25) | 22.5 | x | s |
| 2 | [25,30) | 27.5 | 800 | t |
| 3 | [30,35) | 32.5 | y | 0.40 |
| 4 | [35,40) | 37.5 | 1600 | 0.32 |
| 5 | [40,45) | 42.5 | z | 0.04 |
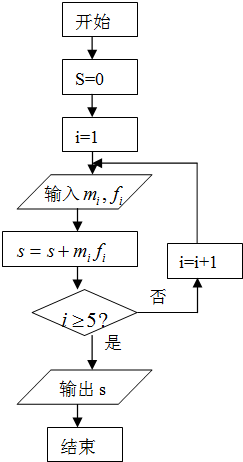
(2)为了对数据进行分析,采用了计算机辅助计算,分析其中一部分计算,见算法流程图,求输出的S值,并说明S的统计意义.
(3)从年龄在[20,30)岁人群中采用分层抽样法抽取6人参加元宵晚会活动,其中选取2人作为代表发言,求选取2名代表中恰有1人年龄在[25,30)岁的概率.
分析:(1)根据公式频率=
及变形公式,即可求解
(2)按照循环结构的运算流程,依次循环运算,最后可求得结果
(3)结合分层抽样的特点(按比例抽样),先算出[20,25)、[25,30)内的人数,然后再分别列举所有可能的情况和符合条件的情况,根据古典概型的概率求法公式即可得解
| 频数 |
| 总数 |
(2)按照循环结构的运算流程,依次循环运算,最后可求得结果
(3)结合分层抽样的特点(按比例抽样),先算出[20,25)、[25,30)内的人数,然后再分别列举所有可能的情况和符合条件的情况,根据古典概型的概率求法公式即可得解
解答:解:(1)依题意则有n=
=5000,y=5000×0.40=2000,z=5000×0.04=200,x=5000-(800+2000+1600+200)=400,s=
=0.08,t=
=0.16
(2)依题意则有S=22.5×0.08+27.5×0.16+32.5×0.40+37.5×0.32+42.5×0.04=32.9
S的统计意义即是指参加调查者的平均年龄
(3)∵[20,25)年龄段与[25,30)年龄段人数的比值为
=
∴采用分层抽样法抽取6人中年龄在[20,25)岁的有2人,年龄在[25,30)岁的有4人,设在[20,25)岁的2人分别为m,n,在[25,30)岁中的4人为a,b,c,d;选取2人作为代表发言的所有可能情况为(a,b),(a,c),(a,d),(a,m),(a,n),(b,c),(b,d),(b,m),(b,n),(c,d),
(c,m),(c,n),(d,m),(d,n),(m,n)共有15种,其中恰有1人在年龄[25,30)岁的代表有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n),(d,m),(d,n)共8种,故概率为P=
| 1600 |
| 0.32 |
| 400 |
| 5000 |
| 800 |
| 5000 |
(2)依题意则有S=22.5×0.08+27.5×0.16+32.5×0.40+37.5×0.32+42.5×0.04=32.9
S的统计意义即是指参加调查者的平均年龄
(3)∵[20,25)年龄段与[25,30)年龄段人数的比值为
| 400 |
| 800 |
| 1 |
| 2 |
∴采用分层抽样法抽取6人中年龄在[20,25)岁的有2人,年龄在[25,30)岁的有4人,设在[20,25)岁的2人分别为m,n,在[25,30)岁中的4人为a,b,c,d;选取2人作为代表发言的所有可能情况为(a,b),(a,c),(a,d),(a,m),(a,n),(b,c),(b,d),(b,m),(b,n),(c,d),
(c,m),(c,n),(d,m),(d,n),(m,n)共有15种,其中恰有1人在年龄[25,30)岁的代表有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n),(d,m),(d,n)共8种,故概率为P=
| 8 |
| 15 |
点评:本题综合考查分层抽样、概率、程序框图等相关知识.要注意分层抽样的特点是按比例抽样,古典概型的求解是某事件所包含的基本事件的个数除以总的基本事件的个数,循环结构要注意循环变量的初值、循环体内的运算顺序、判断条件等.属简单题

练习册系列答案
相关题目
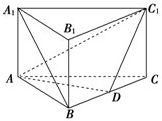 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为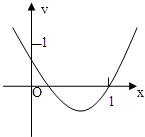 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )