题目内容
已知数列{an}是各项均不为0的等差数列,公差为d,Sn 为其前n项和,且满足an2=S2n-1,n∈N*.数列{bn}满足bn=
,Tn为数列{bn}的前n项和.
(1)求数列{an}的通项公式和Tn;
(2)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn,成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
| 1 |
| anan+1 |
(1)求数列{an}的通项公式和Tn;
(2)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn,成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
(Ⅰ)(法一)在an2=S2n-1,令n=1,n=2可得
即
∴a1=1,d=2
∴an=2n-1
∵bn=
=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)=
(1-
)=
(法二)∵{an}是等差数列,
∴
=an
∴S2n-1=
×(2n-1)=(2n-1)an
由an2=S2n-1,得an2=(2n-1)an,
又an≠0,
∴an=2n-1
∵bn=
=
=
(
-
)
∴Tn=
(1-
+
-
+…+
-
)=
(1-
)=
(Ⅱ)∵T1=
,Tm=
,Tn=
若T1,Tm,Tn,成等比数列,则(
)2=
(
)
即
=
法一:由
=
可得,
=
>0
即-2m2+4m+1>0
∴1-
<m<1+
∵m∈N且m>1
∴m=2,此时n=12
∴当且仅当m=2,n=12时,T1,Tm,Tn,成等比数
法二:∵
=
<
∴
<
∴2m2-4m-1<0
∴1-
<m<1+
∵m∈N且m>1
∴m=2,此时n=12
∴当且仅当m=2,n=12时,T1,Tm,Tn,成等比数
|
即
|
∴a1=1,d=2
∴an=2n-1
∵bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
(法二)∵{an}是等差数列,
∴
| a1+a2n-1 |
| 2 |
∴S2n-1=
| a1+a2n-1 |
| 2 |
由an2=S2n-1,得an2=(2n-1)an,
又an≠0,
∴an=2n-1
∵bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
(Ⅱ)∵T1=
| 1 |
| 3 |
| m |
| 2m+1 |
| n |
| 2n+1 |
若T1,Tm,Tn,成等比数列,则(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
即
| m2 |
| 4m2+4m+1 |
| n |
| 6n+3 |
法一:由
| m2 |
| 4m2+4m+1 |
| n |
| 6n+3 |
| 3 |
| n |
| -2m2+4m+1 |
| m2 |
即-2m2+4m+1>0
∴1-
| ||
| 2 |
| ||
| 2 |
∵m∈N且m>1
∴m=2,此时n=12
∴当且仅当m=2,n=12时,T1,Tm,Tn,成等比数
法二:∵
| n |
| 6n+3 |
| 1 | ||
6+
|
| 1 |
| 6 |
∴
| m |
| 4m2+4m+1 |
| 1 |
| 6 |
∴2m2-4m-1<0
∴1-
| ||
| 2 |
| ||
| 2 |
∵m∈N且m>1
∴m=2,此时n=12
∴当且仅当m=2,n=12时,T1,Tm,Tn,成等比数

练习册系列答案
相关题目
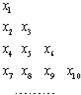 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足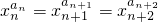 (n∈N*).
(n∈N*).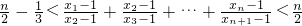 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.