题目内容

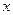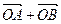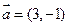已知椭圆的中心为坐标原点O，焦点在轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，与向量共线
（Ⅰ）求椭圆的离心率；
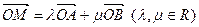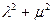（Ⅱ）设M为椭圆上任意一点，且，证明为定值

解：设椭圆方程为
则直线AB的方程为，代入，化简得
.
令A（），B），则
由与共线，得
又，

即，所以，
故离心率
（II）证明：（1）知，所以椭圆可化为
设，由已知得
 在椭圆上，
即①
由（1）知



=0
又，代入①得
故为定值，定值为1

解析

练习册系列答案
相关题目
已知椭圆的中心为坐标原点O，焦点在x轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，
OA
+
OB
与
a
=（3，-1）共线．
（Ⅰ）求椭圆的离心率；
（Ⅱ）设M为椭圆上任意一点，且
OM
=λ
OA
+μ
OB
(λ，μ∈R)，证明λ2+μ2为定值．
已知椭圆的中心为坐标原点O，椭圆短半轴长为1，动点M（2，t）（t＞0）在直线x=
a2c
（a为长半轴，c为半焦距）上．
（1）求椭圆的标准方程
（2）求以OM为直径且被直线3x-4y-5=0截得的弦长为2的圆的方程；
（3）设F是椭圆的右焦点，过点F作OM的垂线与以OM为直径的圆交于点N，求证：线段ON的长为定值，并求出这个定值．
已知椭圆的中心为坐标原点，斜率为1且过椭圆右焦点F（2，0）的直线交椭圆于A，B两点，
OA
+
OB
与
a
=(3，-1)共线，则该椭圆的长半轴长为
6
6
．
已知椭圆的中心为坐标原点O，椭圆短半轴长为1，动点M（2，t）（t＞0）在直线x=
a2c
（a为长半轴，c为半焦距）上．
（1）求椭圆的标准方程；
（2）求以OM为直径且被直线3x-4y-5=0截得的弦长为2的圆的方程．
已知椭圆的中心为坐标原点O，焦点在x轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，
OA
+
OB
与
a
=(3，-1)共线，则该椭圆的离心率为（　　）
A、
5
3
B、
3
2
C、
6
3
D、
2
2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网