题目内容
设函数f(x)=ax-x(a>0,a≠1)(1)若a=e(e是自然对数的底数),求f(x)的单调区间和极值;
(2)若函数y=f(|x|)在全体实数R上恰有4个零点,求实数a的取值范围.
【答案】分析:(1)将a=e代入求出函数解析式,可得导函数的解析式,进而求出f′(x)>0时和f′(x)<0时自变量的范围,得到f(x)的单调区间,同时根据极值的定义,求出极值;
(2)函数y=f(|x|)是偶函数,要使它在全体实数R上恰有4个零点,只须y=f(x)在(0,+∞)上有2个零点,即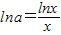 在(0,+∞)有2解,构造函数
在(0,+∞)有2解,构造函数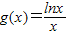 ,利用导数法,可求出满足条件的实数a的取值范围.
,利用导数法,可求出满足条件的实数a的取值范围.
解答:解:(1)f(x)=ex-x,则f′(x)=ex-1…(2分)
当f′(x)>0时,解得x>0,f(x)在[0,+∞)上单调递增,
当f′(x)<0时,解得x<0,f(x)在(-∞,0]上单调递减.…(2分)
所以x=0是极小值点,f极小值=f(0)=1…(2分)
(2)函数y=f(|x|)是偶函数,要使它在全体实数R上恰有4个零点,只须y=f(x)在(0,+∞)上有2个零点,…(2分)
要使方程ax=x在(0,+∞)有2解,则有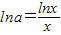 在(0,+∞)有2解,…(2分)
在(0,+∞)有2解,…(2分)
设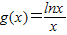 ,则
,则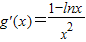 …(1分)
…(1分)
当x>e时,g'(x)<0,g(x)单调递减,且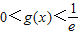
当0<x≤e时,g'(x)>0,g(x)单调递增,且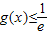 …(4分)
…(4分)
根据图象可知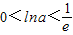 ,
,
∴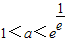 …(2分)
…(2分)
点评:本题考查的知识点是根的存在性及根的个数判断,指数函数的图象和性质,导数法求函数的单调区间及最值,其中熟练掌握利用导数确定函数单调区间和极值的方法步骤是解答的关键.
(2)函数y=f(|x|)是偶函数,要使它在全体实数R上恰有4个零点,只须y=f(x)在(0,+∞)上有2个零点,即
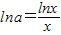 在(0,+∞)有2解,构造函数
在(0,+∞)有2解,构造函数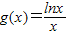 ,利用导数法,可求出满足条件的实数a的取值范围.
,利用导数法,可求出满足条件的实数a的取值范围.解答:解:(1)f(x)=ex-x,则f′(x)=ex-1…(2分)
当f′(x)>0时,解得x>0,f(x)在[0,+∞)上单调递增,
当f′(x)<0时,解得x<0,f(x)在(-∞,0]上单调递减.…(2分)
所以x=0是极小值点,f极小值=f(0)=1…(2分)
(2)函数y=f(|x|)是偶函数,要使它在全体实数R上恰有4个零点,只须y=f(x)在(0,+∞)上有2个零点,…(2分)
要使方程ax=x在(0,+∞)有2解,则有
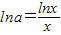 在(0,+∞)有2解,…(2分)
在(0,+∞)有2解,…(2分)设
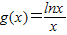 ,则
,则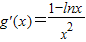 …(1分)
…(1分)当x>e时,g'(x)<0,g(x)单调递减,且
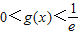
当0<x≤e时,g'(x)>0,g(x)单调递增,且
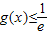 …(4分)
…(4分)根据图象可知
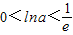 ,
,∴
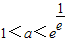 …(2分)
…(2分)点评:本题考查的知识点是根的存在性及根的个数判断,指数函数的图象和性质,导数法求函数的单调区间及最值,其中熟练掌握利用导数确定函数单调区间和极值的方法步骤是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |