题目内容
5.在边长为1的正三角形ABC中,设$\overrightarrow{BC}$=3$\overrightarrow{BD}$,求$\overrightarrow{AD}$•$\overrightarrow{BC}$.分析 建立坐标系,用坐标表示向量,从而解决问题.
解答 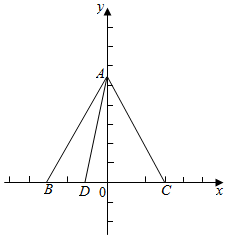 解:建立坐标系,如图所示:
解:建立坐标系,如图所示:
边长为1的正三角形ABC中,设$\overrightarrow{BC}$=3$\overrightarrow{BD}$,
∴A(0,$\frac{\sqrt{3}}{2}$),B(-$\frac{1}{2}$,0),C($\frac{1}{2}$,0),D($-\frac{1}{6}$,0),
∴$\overrightarrow{BC}$=(1,0),$\overrightarrow{AD}$=($-\frac{1}{6}$,-$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{AD}$•$\overrightarrow{BC}$=-$\frac{1}{6}$
故答案为:-$\frac{1}{6}$.
点评 本题考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
15.如图,正方形ABCD中,M是BC的中点,若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BD}$,则λ+μ=( )
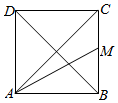

| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{15}{8}$ | D. | 2 |
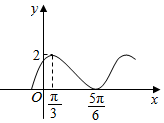 函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.