题目内容
如图,正四面体ABCD的棱AB、AC、AD、BD的中点为K、L、M、N,利用向量证明:(1)AB⊥CD;(2)KL![]() NM.
NM.

证明:正四面体的棱长都相等,|a|=|b|=|c|.
(1) ![]() ·
·![]() =a·(c-b)=a·c-a·b=|a||c|cos60°-|a||b|cos60°=0,
=a·(c-b)=a·c-a·b=|a||c|cos60°-|a||b|cos60°=0,
∴![]() ⊥
⊥![]() ,即AB⊥CD.
,即AB⊥CD.
(2)![]() =
=![]() b-
b-![]() a=
a=![]() (b-a),
(b-a),
![]() =
=![]()
![]() -
-![]()
![]() =
=![]() (b-c)-
(b-c)-![]() (a-c)=
(a-c)=![]() (b-a).∴KL
(b-a).∴KL![]() NM.
NM.

练习册系列答案
相关题目
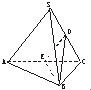 如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )
如图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 9、如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
9、如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( ) 14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题:
14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题: 如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( )
如图:正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( ) 如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为
如图,正四面体S-ABC的边长为a,D是SA的中点,E是BC的中点,则SDE绕SE旋转一周所得旋转体的体积为