题目内容
已知幂函数y=x m2-2m-2(m∈Z)的图象与x轴、y轴都无公共点且是偶函数,求m的值,并画出函数的图象(要求列表)分析:根据幂函数的定义和性质确定m的值,然后作出对应的幂函数的图象.
解答:解:∵幂函数y=x m2-2m-2(m∈Z)的图象、y轴都无公共点,
∴m2-2m-2<0,
即1-
<m<1+
,
∵m∈Z,
∴m=0,1,2.
若m=0,则y=x -2=
为偶函数,满足条件.
若m=1,则y=x-3=
为奇函数,不满足条件,舍去.
若m=2,则y=x -2=
为偶函数,满足条件.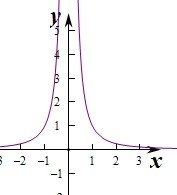
∴m=0或m=2,幂级数y=x -2=
为偶函数.
列表,取值描点得幂函数的图象为:
∴m2-2m-2<0,
即1-
| 3 |
| 3 |
∵m∈Z,
∴m=0,1,2.
若m=0,则y=x -2=
| 1 |
| x2 |
若m=1,则y=x-3=
| 1 |
| x3 |
若m=2,则y=x -2=
| 1 |
| x2 |

∴m=0或m=2,幂级数y=x -2=
| 1 |
| x2 |
列表,取值描点得幂函数的图象为:
| x | -2 | -1 | -
|
|
1 | 2 | 3 | ||||||
| y |
|
1 | 4 | 4 | 1 |
|
|
点评:本题主要考查幂函数的图象和性质,要求熟练掌握幂函数的定义和性质,注意要对m进行分类讨论.

练习册系列答案
相关题目
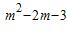 (m∈Z)的图象与x轴y轴都无公共点,且关于y轴对称,则实数m的值是( )
(m∈Z)的图象与x轴y轴都无公共点,且关于y轴对称,则实数m的值是( )