题目内容
己知M={（x，y）|x∈R，y∈R且y≠x+2}，N={（x，y）|x∈R，y∈R且y≠-x}，I={（x，y）|x∈R，y∈R}，则CI（M∪N）= ．
【答案】分析：根据CI（M∪N）=（CIM）∩（CIN），分别求出CIM，CIN，然后求出（CIM）∩（CIN），确定出CI（M∪N）．
解答：解：CI（M∪N）=（CIM）∩（CIN）
CIM=M={（x，y）|x∈R，y∈R且y=x+2}，
CIN={（x，y）|x∈R，y∈R且y=-x}，
（CIM）∩（CIN）={（x，y）|x∈R，y∈R且y=x+2且y=-x}={-1，1}
故答案为：{-1，1}．
点评：本题考查了补集及其运算，应用CI（M∪N）=（CIM）∩（CIN）能将问题简化．
解答：解：CI（M∪N）=（CIM）∩（CIN）
CIM=M={（x，y）|x∈R，y∈R且y=x+2}，
CIN={（x，y）|x∈R，y∈R且y=-x}，
（CIM）∩（CIN）={（x，y）|x∈R，y∈R且y=x+2且y=-x}={-1，1}
故答案为：{-1，1}．
点评：本题考查了补集及其运算，应用CI（M∪N）=（CIM）∩（CIN）能将问题简化．
练习册系列答案
相关题目
-1（其中a是不为0的实数），g（x）=lnx，设F（x）=f（x）+g（x）．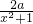
）+2m的图象与函数y=g（x2+1）的图象恰好有四个不同的交点？若存在，求出m的取值范围，若不存在，说明理由．