题目内容
已知集合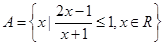 ,集合
,集合 .
.
(1)求集合 ;
;
(2)若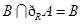 ,求实数
,求实数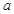 的取值范围.
的取值范围.
(1) ;(2)
;(2)  .
.
解析试题分析:(1)求集合,要认清这个集合的代表元是什么?这个代表元具有什么性质?也即这人集合实质是什么?象本题中集合 实质就是不等式
实质就是不等式 的解集,故我们只要解这个不等式即可,当然分式不等式的解法是移项,把不等式的右边变为0,左边变成若干因式的积或商,再转化为整式不等式,还要注意的转化时要注意等价转化(主要是原分式不等式中分母不能为0);(2)条件
的解集,故我们只要解这个不等式即可,当然分式不等式的解法是移项,把不等式的右边变为0,左边变成若干因式的积或商,再转化为整式不等式,还要注意的转化时要注意等价转化(主要是原分式不等式中分母不能为0);(2)条件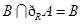 ,说明
,说明 ,不需要求出
,不需要求出 ,而是利用集合的关系解决问题.
,而是利用集合的关系解决问题.
试题解析:解:(1)由 ,得
,得 2分
2分
所以 2分
2分
(2) 2分
2分 2分
2分
由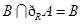 ,得
,得 2分
2分
所以 或
或
所以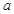 的范围为
的范围为 2分
2分
考点:(1)分式不等式;(2)子集的性质.

练习册系列答案
相关题目
若集合A={x|﹣2<x<1},B={x|0<x<2},则集合A∩B=( )
| A.{x|﹣1<x<1} | B.{x|﹣2<x<1} |
| C.{x|﹣2<x<2} | D.{x|0<x<1} |
集合A={0,1,2,3,4},B={x|x<2},则A∩B=( ).
A. | B.{0,1} | C.{0,1,2} | D.{x|x<2} |
 ( )
( )
A. | B. |
C. | D. |
设集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
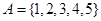
 ,则
,则 中所含元素的个数为 .
中所含元素的个数为 . ,集合
,集合 ,
, .
.
 ,若
,若 ,求实数
,求实数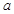 的取值范围.
的取值范围.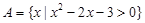 ,
, .
. ,使得
,使得 ,求
,求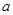 的取值范围;
的取值范围;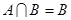 ,求
,求 +
+ +
+ 可能取的值组成的集合是________.
可能取的值组成的集合是________.