题目内容
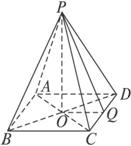
ABCD为正方形,PD⊥平面ABCD,则二面角A-PB-C的大小范围是( )A.(0°,180°) B.(60°,180°]
C.[90°,180°] D.(90°,180°)
答案:D
解析:如图,

作CM⊥PB于点M,连结AM,则AM⊥PB且AM=MC,∠AMC即为所求二面角的平
面角.设正方形边长为a,∠PBC=θ,则AM=CM=asinθ,AC=![]() a.由余弦定理得
a.由余弦定理得
cos∠AMC=![]() =-cot2θ.
=-cot2θ.
在Rt△PBC中,∵0<θ<![]() ,∴cot2θ>0,cos∠AMC<0.
,∴cot2θ>0,cos∠AMC<0.
∴∠AMC为钝角.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD=1.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD=1.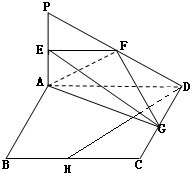 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
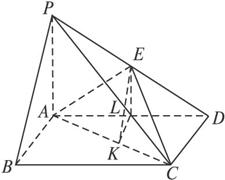
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB,G为PD中点,E为AB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB,G为PD中点,E为AB的中点.