题目内容
设椭圆C1：
的左、右焦点分别是F1，F2，下顶点为A，线段OA的中点为B(O为坐标原点)，如图．若抛物线C2：y＝x2－1与y轴的交点为B，且经过F1，F2点．
(1)求椭圆C1的方程；
(2)设
，N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于，P，Q两点，求△MPQ面积的最大值．
答案：
解析：
解析：
|
解：(1)由题意可知B(0，－1)，则A(0，－2)，故b＝2． 令y＝0得 所以 (2)设N( 代入椭圆方程整理得： 故 设点M到直线PQ的距离为d，则 所以， 当 综上可知， |
即
，则F1(－1，0)，F2(1，0)，故c＝1．
．于是椭圆C1的方程为：
．
)，由于
知直线PQ的方程为：
．即
．
，
＝
，
，
，
．
．
的面积S
时取到“＝”，经检验此时
，满足题意．
的面积的最大值为
．
练习册系列答案
相关题目
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：
与
轴的交点为B，且经过F1，F2点．
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值．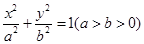
与y轴的交点为B，且经过F1，F2点．
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值．
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：
与y轴的交点为B，且经过F1，F2点。
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值。
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点）。如图，若抛物线C2：
与y轴的交点为B，且经过F1，F2两点。
，N为抛物线C2上的动点，过点N作抛物线C2的切线交椭圆C1于点P、Q两点，求△MPQ面积的最大值。
的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图。若抛物线C2：
与y轴的交点为B，且经过F1，F2点
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求
面积的最大值。