题目内容
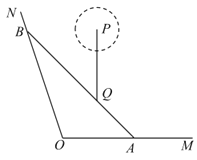
【题目】我市为迎接一项重要的体育赛事，要完成
，
两座场馆的地基建造工程.某工程队需要把600名工人分成两组，一组完成场馆的甲级标准地基2000
，同时另一组完成场馆的乙级标准地基3000；据测算，完成甲级标准地基每平方米的工程量为50人
天，完成乙级标准地基每平方米的工程量为30人天.
（1）若工程队分配
名工人去场馆，求场馆地基和场馆地基建造时间
和
（单位：天）的函数解析式；
（2）、两个场馆同时开工，该工程队如何分配两个场馆的工人数量，可以使得工期最短.
（参考数据：
，
，
.备注：若地基面积为
平方米，每平方米的工程量为
人/天，工人数
人，则工期为
天.）
【答案】(1)
；(2) 分配
名工人去
场馆，
名工人去
场馆.
【解析】
（1）根据题意，以及备注内容，即可分别求出
的解析式；
（2）由（1）中所求，结合函数的单调性，要使得工期最短，只需
，解方程即可求得.
（1）场馆的面积为2000
，每平方米的工程量为50人/天，现有
名工人，
故可得场馆地基建造时间
；
场馆的面积为3000，平方米的工程量为30人/天，现有
名工人，
故可得场馆地基建造时间
；
综上所述：
.
（2）设工期为
，则
，其中
.
容易知
是单调减函数，
是单调增函数，
故当且仅当两个场馆同时完工时，工期最短.
令，即可得
，
解得
.
故分配名工人去场馆，名工人去场馆工期最短.
【题目】为了解某班学生喜爱打篮球是否与性别有关，对该班40名学生进行了问卷调查，得到了如下的
列联表：
男生 | 女生 | 总计 | |
喜爱打篮球 | 19 | 15 | 34 |
不喜爱打篮球 | 1 | 5 | 6 |
总计 | 20 | 20 | 40 |
（1）在女生的20个个体中，随机抽取2人，记随机变量
为抽到“不喜爱篮球”的人数，求的分布列及数学期望
；
（2）判断能否在犯错误的概率不超过0.1的条件下认为喜爱篮球与性别有关？
附：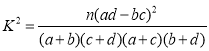
，其中
．
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来，随着国家综合国力的提升和科技的进步，截至
年底，中国铁路运营里程达
万千米，这个数字比
年增长了
倍；高铁运营里程突破
万千米，占世界高铁运营里程的
以上，居世界第一位．如表截取了
年中国高铁密度的发展情况（单位：千米/万平方千米）．
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
高铁密度 |
|
|
|
|
|
已知高铁密度
与年份代码
之间满足关系式
（
为大于
的常数）．
（1）根据所给数据，求关于的回归方程（精确到
位）；
（2）利用（1）的结论，预测到哪一年，高铁密度会超过
千米/万平方千米．
参考公式：设具有线性相关系的两个变量
的一组数据为
，则回归方程
的系数：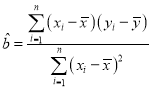
，
参考数据：
，
，
，
，
，
．
【题目】已知某保险公司的某险种的基本保费为
（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | ≥4 |
保费（元） |
|
|
|
|
|
随机调查了该险种的
名续保人在一年内的出险情况，得到下表：
出险次数 | 0 | 1 | 2 | 3 | ≥4 |
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下：
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额（元） |
|
|
|
|
|
将所抽样本的频率视为概率.
（1）求本年度续保人保费的平均值的估计值；
（2）按保险合同规定，若续保人在本年度内出险
次，则可获得赔付
元；依此类推，求本年度续保人所获赔付金额的平均值的估计值；
（3）续保人原定约了保险公司的销售人员在上午
之间上门签合同，因为续保人临时有事，外出的时间在上午
之间，请问续保人在离开前见到销售人员的概率是多少？
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况，对2019年元旦期间的90位游客购买情况进行统计，得到如下人数分布表.
购买金额（元） |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
（1）根据以上数据完成
列联表，并判断是否有
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
（2）为吸引游客，该超市推出一种优惠方案，购买金额不少于60元可抽奖3次，每次中奖概率为
（每次抽奖互不影响，且的值等于人数分布表中购买金额不少于60元的频率），中奖1次减5元，中奖2次减10元，中奖3次减15元.若游客甲计划购买80元的土特产，请列出实际付款数
（元）的分布列并求其数学期望.
附：参考公式和数据：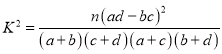
，
.
附表：
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
