题目内容

已知命题p：方程x2+mx+1=0有两个不等的负实数根.命题q：方程4x2+4(m-2)x+1=0无实数根.若“p或q”为真命题，“p且q”为假命题，求m的取值范围.

解析：先将p、q中m的范围求出，然后根据“p或q”为真，“p且q”为假，可知p和q中必是一真一假，则分两种情况列出不等式组求解.由p得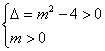则m＞2,由q知，Δ′=16(m-2)2-16=16(m2-4m+3)＜0,则1＜m＜3

于是有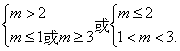解得m≥3或1＜m≤2

练习册系列答案
相关题目
已知命题p：方程x2+mx+1=0有两个不等的负实根；q：方程mx2+（m-1）x+m=0无实根．若“p或q”为真，p且q”为假，求实数m的取值范围．
已知命题P：方程x2+mx+1=0有两个不相等的负实数根；命题Q：函数f（x）=lg[4x2+（m-2）x+1]的定义域为实数集R，若P或Q为真，P且Q为假，求实数m的取值范围．
已知命题P：“方程x2+
y2m
=1表示焦点在y轴上的椭圆”；命题Q：“方程2x2-4x+m=0没有实数根”．若P∧Q假，P∨Q为真，求实数m的取值范围．
已知命题P：方程x2-2mx+m=0没有实数根；
命题Q：?x∈R，x2+mx+1≥0．
（1）写出命题Q的否定“￢Q”；
（2）如果“P∨Q”为真命题，“P∧Q”为假命题，求实数m的取值范围．
已知命题p：方程x2+mx+1=0有两个不等的正实数根，命题q：方程4x2+4（m+2）x+1=0无实数根．
（1）若p为真命题，求m的取值范围；
（2）若q为真命题，求m的取值范围；
（3）若“p或q”为真命题，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网