题目内容
函数y=f(x)=ax+b满足f(0)=1且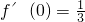
(1)求f(x)的解析式.
(2)试判断函数y=f(x)的图象与直线y=x有无交点,并证明你的判断.
解:(1)f'(x)=axlna,依题意得 f(0)=a0+b=1,
f(0)=a0+b=1,
解得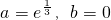 ,
,
∴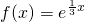 …(4分)
…(4分)
(2)函数y=f(x)的图象与直线y=x有两交点.…(6分)
证明: ,
,
令g(x)= ,
,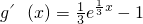
令g'(x)=0,解得x=3ln3
g'(x)>0,解得x>3ln3
g'(x)<0,得x<3ln3
所以g(x)min=g(3ln3)=3-3ln3<0…(9分)
显然g(6)═e2-6>0,又g(x) 在(3ln3,+∞)上是增函数,
∴g(x)= 在(3ln3,+∞)上有一个根.…(11分)
在(3ln3,+∞)上有一个根.…(11分)
而g(-3)═e-1+3>0,又g(x) 在(-∞,3ln3)上是减函数,
∴g(x)= 在(-∞,3ln3)上有一个根.…(13分)
在(-∞,3ln3)上有一个根.…(13分)
综上所述函数y=f(x)的图象与直线y=x有两交点.…(14分)
分析:(1)先求出其导函数,再结合f(0)=1以及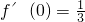 得到关于a和b的方程,求出a和b的值即可求f(x)的解析式;
得到关于a和b的方程,求出a和b的值即可求f(x)的解析式;
(2)先根据条件把判断函数y=f(x)的图象与直线y=x有无交点问题转化为f(x)=x有无根的问题;再构造出函数出g(x)= ,根据其导函数研究出其最值及其单调性即可的出结论.
,根据其导函数研究出其最值及其单调性即可的出结论.
点评:本题主要考查导函数的应用以及指数函数的综合问题.解决第二问的关键在于把判断函数y=f(x)的图象与直线y=x有无交点问题转化为方程f(x)=x有无根的问题.
 f(0)=a0+b=1,
f(0)=a0+b=1,解得
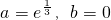 ,
,∴
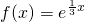 …(4分)
…(4分)(2)函数y=f(x)的图象与直线y=x有两交点.…(6分)
证明:
 ,
,令g(x)=
 ,
,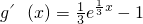
令g'(x)=0,解得x=3ln3
g'(x)>0,解得x>3ln3
g'(x)<0,得x<3ln3
所以g(x)min=g(3ln3)=3-3ln3<0…(9分)
显然g(6)═e2-6>0,又g(x) 在(3ln3,+∞)上是增函数,
∴g(x)=
 在(3ln3,+∞)上有一个根.…(11分)
在(3ln3,+∞)上有一个根.…(11分)而g(-3)═e-1+3>0,又g(x) 在(-∞,3ln3)上是减函数,
∴g(x)=
 在(-∞,3ln3)上有一个根.…(13分)
在(-∞,3ln3)上有一个根.…(13分)综上所述函数y=f(x)的图象与直线y=x有两交点.…(14分)
分析:(1)先求出其导函数,再结合f(0)=1以及
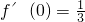 得到关于a和b的方程,求出a和b的值即可求f(x)的解析式;
得到关于a和b的方程,求出a和b的值即可求f(x)的解析式;(2)先根据条件把判断函数y=f(x)的图象与直线y=x有无交点问题转化为f(x)=x有无根的问题;再构造出函数出g(x)=
 ,根据其导函数研究出其最值及其单调性即可的出结论.
,根据其导函数研究出其最值及其单调性即可的出结论.点评:本题主要考查导函数的应用以及指数函数的综合问题.解决第二问的关键在于把判断函数y=f(x)的图象与直线y=x有无交点问题转化为方程f(x)=x有无根的问题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
②函数f(x)在[0,1]是减函数,在[1,2]是增函数; ③当1<a<2时,函数y=f(x)-a有4个零点; ④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最小值为0, 其中所有正确命题的个数是( ) |
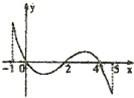 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示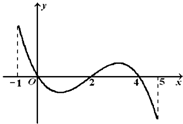

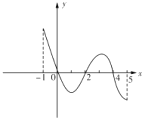 (2013•湖南模拟)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.
(2013•湖南模拟)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.