题目内容

已知函数f(x)=2asin2x-2asinx·cosx+a+b(a≠0)的定义域为［0,］,值域为［-5,1］,求常数a、b的值.

剖析:首先通过三角恒等变形,将函数化成一个角的一种函数的形式,然后注意函数定义域对确定函数的值域的影响.

解:f(x)=a(1-cos2x)-asin2x+a+b

    =-a(cos2x+sin2x)+2a+b

    =-2asin(2x+)+2a+b.

    ∵x∈［0,］,∴2x+∈［,］.

    ∴-≤sin(2x+)≤1.

    因此,由f(x)的值域为［-5,1］可得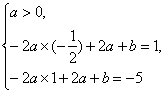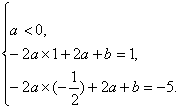

   

    或

    ∴或

讲评:本题主要考查了有范围的三角函数最值的求法,解决本题的关键是对参数的讨论.

练习册系列答案
相关题目
已知函数f(x)=
2-xx+1
；
（1）求出函数f（x）的对称中心；
（2）证明：函数f（x）在（-1，+∞）上为减函数；
（3）是否存在负数x0，使得f(x0)=3x0成立，若存在求出x0；若不存在，请说明理由．
已知函数f(x)=
2-x-1，x≤0
x
，x＞0
，则f[f（-2）]=
3
3
．
已知函数f(x)=2(sin2x+
3
2
)cosx-sin3x
（1）求函数f（x）的值域和最小正周期；
（2）当x∈[0，2π]时，求使f(x)=
3
成立的x的值．
已知函数f(x)=2-
ax+1
(a∈R)的图象过点（4，-1）
（1）求a的值；
（2）求证：f（x）在其定义域上有且只有一个零点；
（3）若f（x）+mx＞1对一切的正实数x均成立，求实数m的取值范围．
已知函数f(x)=
2-2cosx
+
2-2cos(
2π
3
-x)
，x∈[0，2π]，则当x=
4π
3
4π
3
时，函数f（x）有最大值，最大值为
2
3
2
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网