题目内容
已知函数![]() 当
当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
![]() 对任意正数
对任意正数![]() ,证明:
,证明:![]() .
.
解:![]() 当
当![]() 时,
时,![]() ,求导得
,求导得  ,
,
于是当![]() 时,
时,![]() ;而当
;而当 ![]() 时,
时,![]() .
.
即![]() 在
在![]() 中单调递增,而在
中单调递增,而在![]() 中单调递减.
中单调递减.
(2)对任意给定的![]() ,
,![]() ,由
,由 ,
,
若令 ![]() ,则
,则 ![]() … ① ,
… ① ,![]() … ②
… ②
(一)先证![]() ;因为
;因为![]() ,
,![]() ,
,![]() ,
,
又由 ![]() ,得
,得 ![]() .
.
所以![]()
![]()
![]()
![]() .
.
(二)再证![]() ;由①、②式中关于
;由①、②式中关于![]() 的对称性,不妨设
的对称性,不妨设![]() .则
.则![]()
(Ⅰ)当![]() ,则
,则![]() ,所以
,所以![]() ,因为
,因为 ![]() ,
,
![]() ,此时
,此时![]() .
.
(Ⅱ)当![]() …③,由①得 ,
…③,由①得 ,![]() ,
,![]() ,
,
因为 ![]() 所以
所以 ![]() … ④
… ④
同理得![]() … ⑤ ,于是
… ⑤ ,于是  … ⑥
… ⑥
今证明 ![]() … ⑦, 因为
… ⑦, 因为 ![]() ,
,
只要证 ![]() ,即
,即 ![]() ,也即
,也即 ![]() ,据③,此为显然.
,据③,此为显然.
因此⑦得证.故由⑥得 ![]() .
.
综上所述,对任何正数![]() ,皆有
,皆有![]() .
.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目

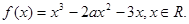
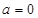 时,求函数
时,求函数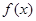 的极大值和极小值;
的极大值和极小值;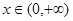 时,
时,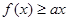 恒成立,求
恒成立,求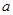 的取值范围.
的取值范围.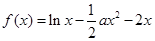 .
.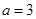 时,求函数
时,求函数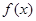 的极大值;
的极大值;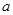 的取值范围.
的取值范围. .
. 时,求
时,求 的极值;
的极值; 时,求
时,求 ,
, 时,求
时,求 的反函数
的反函数 ;
; 的函数
的函数 当
当 时的最小值
时的最小值 ;
; ①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间
①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间 使得函数在区间
使得函数在区间 上的值域为
上的值域为 .
. 是否为“和谐函数”?若是,求出
是否为“和谐函数”?若是,求出 的值或关系式;若不是,请说明理由;
的值或关系式;若不是,请说明理由; 是“和谐函数”,求实数
是“和谐函数”,求实数 的取值范围.
的取值范围.