题目内容
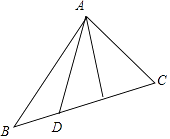
【题目】△ABC中,sin(A﹣B)=sinC﹣sinB,D是边BC的一个三等分点(靠近点B),记 ![]() ,则当λ取最大值时,tan∠ACD= .
,则当λ取最大值时,tan∠ACD= .
【答案】2+ ![]()
【解析】解:∵sin(A﹣B)=sinC﹣sinB, ∴sinAcosB﹣cosAsinB=sinC﹣sinB=sinAcosB+cosAsinB﹣sinB,
∴sinB=2cosAsinB,∵sinB≠0,
∴cosA= ![]() ,由A∈(0,π),可得:A=
,由A∈(0,π),可得:A= ![]() ,
,
在△ADB中,由正弦定理可将 ![]() ,变形为则
,变形为则 ![]() ,
,
∵ ![]() =
= ![]()
∴ ![]() 即a2λ2=4c2+b2+2bc…①
即a2λ2=4c2+b2+2bc…①
在△ACB中,由余弦定理得:a2=b2+c2﹣bc…②
由①②得 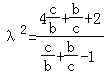
令 ![]() ,
, 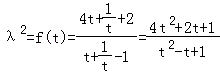 ,f′(t)=
,f′(t)= ![]() ,令f′(t)=0,得t=
,令f′(t)=0,得t= ![]() ,
,
即 ![]() 时,λ最大.
时,λ最大.
结合②可得b= ![]() ,a=
,a= ![]() c
c
在△ACB中,由正弦定理得 ![]()
![]() ,tanC=2+
,tanC=2+ ![]()
所以答案是:2+ ![]() .
.
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目