题目内容
“ ”是“一元二次方程x2+x+m=0有实数解”的
”是“一元二次方程x2+x+m=0有实数解”的
- A.充分非必要条件
- B.充分必要条件
- C.必要非充分条件
- D.非充分非必要条件
A
分析:利用充分必要条件的判断法判断这两个条件的充分性和必要性.关键看二者的相互推出性.
解答:由x2+x+m=0知, ?
?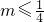 .
.
(或由△≥0得1-4m≥0,∴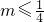 .)
.)
 ,
,
反之“一元二次方程x2+x+m=0有实数解”必有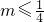 ,未必有m
,未必有m ,
,
因此“ ”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件.
”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件.
故选A.
点评:本题考查充分必要条件的判断性,考查二次方程有根的条件,注意这些不等式之间的蕴含关系.
分析:利用充分必要条件的判断法判断这两个条件的充分性和必要性.关键看二者的相互推出性.
解答:由x2+x+m=0知,
 ?
?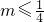 .
.(或由△≥0得1-4m≥0,∴
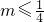 .)
.)
 ,
,反之“一元二次方程x2+x+m=0有实数解”必有
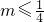 ,未必有m
,未必有m ,
,因此“
 ”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件.
”是“一元二次方程x2+x+m=0有实数解”的充分非必要条件.故选A.
点评:本题考查充分必要条件的判断性,考查二次方程有根的条件,注意这些不等式之间的蕴含关系.

练习册系列答案
相关题目
已知α,β∈(0,
),且tanα,tanβ是一元二次方程x2-3
x+4=0的两个实根,则α+β=( )
| π |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|