题目内容
已知f(x)是个一元三次函数,且满足
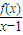 =4,
=4,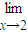
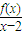 =-2,若函数F(x)=
=-2,若函数F(x)=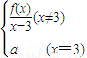 在R上处处连续,则实数a的值为 .
在R上处处连续,则实数a的值为 .
【答案】分析:设f(x)=mx3+nx2+px+q,由
 =4,知m+n+p+q=0,m+(n+m)+(p+m+n)=4,由
=4,知m+n+p+q=0,m+(n+m)+(p+m+n)=4,由
 =-2,知8m+4n+2p+q=0,4m+2(n+2m)+(p+2n+4m)=-2,由此求得f(x)=2x3-12x2+22x-12.再由
=-2,知8m+4n+2p+q=0,4m+2(n+2m)+(p+2n+4m)=-2,由此求得f(x)=2x3-12x2+22x-12.再由 =
= =4,知F(3)=a=4.
=4,知F(3)=a=4.
解答:解:∵f(x)是个一元三次函数,
∴设f(x)=mx3+nx2+px+q,
∵
 =4,
=4,
∴m+n+p+q=0,
且f(x)=(x-1)[mx2+(n+m)x+(p+m+n)],
∴m+(n+m)+(p+m+n)=4,
p+m+n=-q.
∵
 =-2,
=-2,
∴8m+4n+2p+q=0,
且f(x)=(x-2)[mx2+(n+2m)x+(p+2n+4m)]
∴4m+2(n+2m)+(p+2n+4m)=-2,
-2(p+2n+4m)=q.
∴m=2,n=-12,p=22,q=-12.
∴f(x)=2x3-12x2+22x-12,
∵
=
=4
∴若函数F(x)= 在R上处处连续,
在R上处处连续,
则F(3)=a=4.
故答案为:4.
点评:本题考查极限的运算和应用,解题时要理解极限的概念,注意函数F(x)= 在R上处处连续的成立条件.
在R上处处连续的成立条件.

 =4,知m+n+p+q=0,m+(n+m)+(p+m+n)=4,由
=4,知m+n+p+q=0,m+(n+m)+(p+m+n)=4,由
 =-2,知8m+4n+2p+q=0,4m+2(n+2m)+(p+2n+4m)=-2,由此求得f(x)=2x3-12x2+22x-12.再由
=-2,知8m+4n+2p+q=0,4m+2(n+2m)+(p+2n+4m)=-2,由此求得f(x)=2x3-12x2+22x-12.再由 =
= =4,知F(3)=a=4.
=4,知F(3)=a=4.解答:解:∵f(x)是个一元三次函数,
∴设f(x)=mx3+nx2+px+q,
∵

 =4,
=4,∴m+n+p+q=0,
且f(x)=(x-1)[mx2+(n+m)x+(p+m+n)],
∴m+(n+m)+(p+m+n)=4,
p+m+n=-q.
∵

 =-2,
=-2,∴8m+4n+2p+q=0,
且f(x)=(x-2)[mx2+(n+2m)x+(p+2n+4m)]
∴4m+2(n+2m)+(p+2n+4m)=-2,
-2(p+2n+4m)=q.
∴m=2,n=-12,p=22,q=-12.
∴f(x)=2x3-12x2+22x-12,
∵

=

=4
∴若函数F(x)=
 在R上处处连续,
在R上处处连续,则F(3)=a=4.
故答案为:4.
点评:本题考查极限的运算和应用,解题时要理解极限的概念,注意函数F(x)=
 在R上处处连续的成立条件.
在R上处处连续的成立条件. 
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目