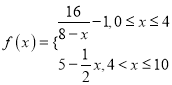题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值和单调区间;
的极值和单调区间;
(2)若在区间![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值是![]() ,
,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)借助题设条件运用导数求解;(2)先借助导数分类讨论求出最值,再建立不等式求解.
试题解析:
(1)当![]() ,
,
令![]() ,得
,得![]() ,
,
又![]() 的定义域为
的定义域为![]() ,由
,由![]() 得
得![]() ,由
,由![]() ,得
,得![]() ,
,
所以![]() 时,
时,![]() 有极小值为1,
有极小值为1,
![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)![]() ,且
,且![]() ,令
,令![]() ,得到
,得到![]() ,若在区间
,若在区间![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,即
成立,即![]() 在区间
在区间![]() 上的最小值小于0.
上的最小值小于0.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() .
.
当![]() ,即
,即![]() 时,
时,
①若![]() ,则
,则![]() 对
对![]() 成立,所以
成立,所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
显然,![]() 在区间
在区间![]() 上的最小值小于0不成立,
上的最小值小于0不成立,
②若![]() ,即
,即![]() 时,则有
时,则有
|
|
|
|
|
| 0 |
|
|
| 极小值 |
|
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,即
,即![]() ,
,
综上,由①②可知:![]() 符合题意.
符合题意.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】铁矿石A和B的含铁率为![]() ,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
的价格c如下表:
| b(万吨) |
| |
A | 50% | 1 | 3 |
B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).