题目内容
如图,已知四棱锥P-ABCD的底面为菱形,PA=PC=2,PB=PD,∠BAC=60°,若O是AC与BD的交点.(1)求证:PO⊥面ABCD;
(2)若BC=2,OM⊥CD于M,求PM与面ABCD所成角的正切.
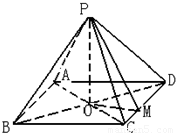
【答案】分析:(1)由四棱锥P-ABCD的底面为菱形,PA=PC=2,PB=PD,O是AC与BD的交点,知PO⊥AC,PO⊥BD,由此能够证明PO⊥面ABCD.
(2)由四棱锥P-ABCD的底面为菱形,PA=PC=2,∠BAC=60°,BC=2,知△ABC是等边三角形,由题设条件能推导出∠PMO是PM与平面ABCD所成的角,由此能求出PM与面ABCD所成角的正切值.
解答:解:(1)∵四棱锥P-ABCD的底面为菱形,PA=PC=2,PB=PD,O是AC与BD的交点,
∴BO=DO,AO=CO,
∴PO⊥AC,PO⊥BD,
又∵AC∩BD=0,∴PO⊥面ABCD.
(2)∵四棱锥P-ABCD的底面为菱形,PA=PC=2,∠BAC=60°,BC=2,
∴△ABC是等边三角形,AC⊥BD,∴AC=2,BO=DO=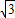 ,
,
∴PO=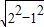 =
=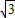 ,
,
∵OM⊥CD于M,∴OM=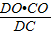 =
=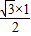 =
=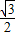 ,
,
∵PO⊥面ABCD,∴∠PMO是PM与平面ABCD所成的角,
由上tan∠PMO=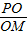 =
=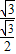 =2.
=2.
故PM与面ABCD所成角的正切值为2.
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正切值的求法,解题时要认真审题,仔细解答,注意培养空间思维能力.
(2)由四棱锥P-ABCD的底面为菱形,PA=PC=2,∠BAC=60°,BC=2,知△ABC是等边三角形,由题设条件能推导出∠PMO是PM与平面ABCD所成的角,由此能求出PM与面ABCD所成角的正切值.
解答:解:(1)∵四棱锥P-ABCD的底面为菱形,PA=PC=2,PB=PD,O是AC与BD的交点,
∴BO=DO,AO=CO,
∴PO⊥AC,PO⊥BD,
又∵AC∩BD=0,∴PO⊥面ABCD.
(2)∵四棱锥P-ABCD的底面为菱形,PA=PC=2,∠BAC=60°,BC=2,
∴△ABC是等边三角形,AC⊥BD,∴AC=2,BO=DO=
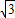 ,
,∴PO=
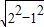 =
=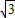 ,
,∵OM⊥CD于M,∴OM=
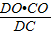 =
=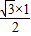 =
=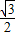 ,
,∵PO⊥面ABCD,∴∠PMO是PM与平面ABCD所成的角,
由上tan∠PMO=
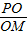 =
=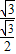 =2.
=2.故PM与面ABCD所成角的正切值为2.
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正切值的求法,解题时要认真审题,仔细解答,注意培养空间思维能力.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,