题目内容
已知a,b,c分别是△ABC三内角A,B,C所对的边,向量 =(-1,
=(-1, ),
), =(cosA,sinA),且
=(cosA,sinA),且 =1.
=1.
(1)求角A;
(2)若a=4,△ABC的面积为 ,求b,c的值.
,求b,c的值.
解:(1)由题意可得  =-cosA+
=-cosA+ sinA=2sin(A-
sinA=2sin(A- )=1,故有 sin(A-
)=1,故有 sin(A- )=
)= .
.
再由0<A<π可得 A- =
= ,∴A=
,∴A= .
.
(2)∵a=4,△ABC的面积为 ,∴
,∴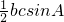 =4
=4 ,∴bc=16.
,∴bc=16.
再由余弦定理可得 a2=b2+c2-2bc•cosA=b2+c2-16=16,
故有 b2+c2=32.与bc=16联立,解得 b=c=4.
分析:(1)由 =1,利用两个向量的数量积公式以及两角差的正弦公式求得 sin(A-
=1,利用两个向量的数量积公式以及两角差的正弦公式求得 sin(A- )=
)= .再由0<A<π可得 A的值.
.再由0<A<π可得 A的值.
(2)由a=4,△ABC的面积为 ,求得 bc=16.再由余弦定理求得b2+c2=32,由此求得b,c的值.
,求得 bc=16.再由余弦定理求得b2+c2=32,由此求得b,c的值.
点评:本题主要考查两个向量的数量积公式、两角差的正弦公式、两个向量夹角公式以及余弦定理的应用,属于中档题.
 =-cosA+
=-cosA+ sinA=2sin(A-
sinA=2sin(A- )=1,故有 sin(A-
)=1,故有 sin(A- )=
)= .
.再由0<A<π可得 A-
 =
= ,∴A=
,∴A= .
.(2)∵a=4,△ABC的面积为
 ,∴
,∴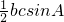 =4
=4 ,∴bc=16.
,∴bc=16.再由余弦定理可得 a2=b2+c2-2bc•cosA=b2+c2-16=16,
故有 b2+c2=32.与bc=16联立,解得 b=c=4.
分析:(1)由
 =1,利用两个向量的数量积公式以及两角差的正弦公式求得 sin(A-
=1,利用两个向量的数量积公式以及两角差的正弦公式求得 sin(A- )=
)= .再由0<A<π可得 A的值.
.再由0<A<π可得 A的值.(2)由a=4,△ABC的面积为
 ,求得 bc=16.再由余弦定理求得b2+c2=32,由此求得b,c的值.
,求得 bc=16.再由余弦定理求得b2+c2=32,由此求得b,c的值.点评:本题主要考查两个向量的数量积公式、两角差的正弦公式、两个向量夹角公式以及余弦定理的应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目