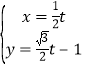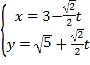题目内容
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为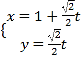 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求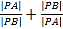 的值.
的值.
【答案】(1)![]() ;
;![]() ;(2)4
;(2)4
【解析】
(1)直接消去参数,将直线![]() 的参数方程化为普通方程,利用互化公式将曲线
的参数方程化为普通方程,利用互化公式将曲线![]() 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(2)将直线的参数方程代入曲线![]() 的普通方程,得到
的普通方程,得到![]() ,得出
,得出![]() ,
,![]() ,化简
,化简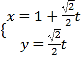 ,代入韦达定理,即可求出结果.
,代入韦达定理,即可求出结果.
解:(1)![]() 的参数方程消去参数,易得
的参数方程消去参数,易得![]() 的普通方程为
的普通方程为![]() ,
,
曲线![]() :
:![]() ,
,
即![]() ,
,
∴![]() ,
,
所以曲线![]() 的直角坐标方程为:
的直角坐标方程为:![]() .
.
(2)![]() 的参数方程
的参数方程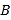 (
(![]() 为参数),
为参数),
设![]() 对应参数为
对应参数为![]() ,
,![]() 对应参数为
对应参数为![]() ,
,
将![]() 的参数方程与
的参数方程与![]() 联立得:
联立得:![]() ,
,
得:![]() ,
,![]() ,
,
所以![]()
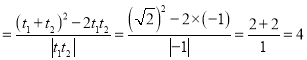
即![]() .
.

练习册系列答案
相关题目
【题目】
|
某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
P(A);
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]()