题目内容
设△ABC的三个内角为A,B,C,向量m=(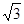 sinA,sinB),n=(cosB,
sinA,sinB),n=(cosB,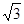 cosA),若m·n=1+cos(A+B),则C=( )
cosA),若m·n=1+cos(A+B),则C=( )
A.  B.
B. 
C.  D.
D. 
C
解析

练习册系列答案
相关题目
已知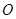 为平面上的定点,
为平面上的定点,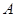 、
、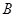 、
、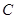 是平面上不共线的三点,若
是平面上不共线的三点,若
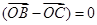 ,则DABC是( )
,则DABC是( )
| A.以AB为底边的等腰三角形 | B.以BC为底边的等腰三角形 |
| C.以AB为斜边的直角三角形 | D.以BC为斜边的直角三角形 |
已知向量 ,
, ,若
,若 ∥
∥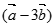 ,则实数k的取值为( )
,则实数k的取值为( )
A. | B. | C. | D. . . |
已知两个非零向量 满足
满足 ,则下面结论正确
,则下面结论正确
A. | B. | C. | D. |
已知向量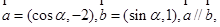 则
则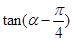 等于( )
等于( )
A.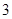 | B.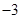 | C. | D.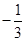 |
已知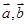 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么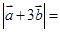
A. | B.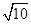 | C. | D. |
已知向量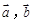 满足
满足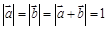 ,则向量
,则向量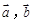 夹角的余弦值为( )
夹角的余弦值为( )
A.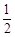 | B. | C.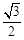 | D.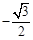 |
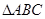 的外接圆的圆心为O,半径为1,
的外接圆的圆心为O,半径为1,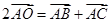 且
且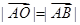 ,则向量
,则向量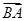 在向量
在向量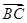 方向上的投影为( )
方向上的投影为( )
A.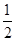 | B.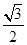 | C.-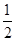 | D.-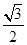 |
 中,已知
中,已知 ,
, ,
,
 ,
, ,则
,则 的值是 .
的值是 .