Question

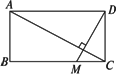
如图所示，一个矩形花园里需要铺两条笔直的小路，已知矩形花园长AD＝5 m，宽AB＝3 m，其中一条小路定为AC，另一条小路过点D，问如何在BC上找到一点M，使得两条小路AC与DM相互垂直？

Answer 1

答案：
解析：

　　解法一：以点B为原点，BC、BA所在直线分别为x、y轴建立直角坐标系(如图所示)，由AD＝5，AB＝3，可得C(5，0)、D(5，3)、A(0，3)．

　　∴直线AC的方程为＝1，即3x＋5y－15＝0．设过点D(5，3)与直线AC垂直的直线方程为5x－3y＝t，由t＝25－9＝16，即得过点D(5，3)与直线AC垂直的直线方程为5x－3y－16＝0．

　　令y＝0，得x＝＝3.2，即BM＝3.2 m时，两条小路AC与DM相互垂直．

　　解法二：以点B为原点，BC、BA所在直线分别为x、y轴建立直角坐标系(如图所示)，由AD＝5，AB＝3，可得C(5，0)、D(5，3)、A(0，3)，设点M的坐标为(x，0)，∵AC⊥DM，∴k_AC·k_DM＝－1．

　　∴＝－1，即x＝5＝3.2，即BM＝3.2 m时，两条小路AC与DM相互垂直．