题目内容
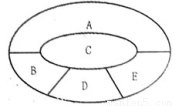
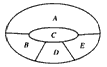
 如图,某学校要用鲜花布置花圃中A,B,C,D,E五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同的颜色的鲜花,现有红,黄,蓝,白,紫五种不同颜色的鲜花可供任意选择,记X表示花圃中用红色鲜花布置的区域的个数,则随机变量X的期望EX=________.
如图,某学校要用鲜花布置花圃中A,B,C,D,E五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同的颜色的鲜花,现有红,黄,蓝,白,紫五种不同颜色的鲜花可供任意选择,记X表示花圃中用红色鲜花布置的区域的个数,则随机变量X的期望EX=________.
1
分析:由题意知花圃中红色鲜花区域的块数可能为0,1,2,当ξ=0时,表示用黄、蓝、白、橙四种颜色来涂色,ξ=2表示恰有两个区域用红色鲜花”,求出相应的概率即可求得期望.
解答:由题意可得随机变量ξ的取值分别为0,1,2.
则当ξ=0时,表示用黄、蓝、白、橙四种颜色来涂色,
若A、D为同色时,共有4×3×2×1×2=48种;
若A、D为不同色时,共有4×3×2×1×1=24种;
即ξ=0所包含的基本事件有48+24=72种,
所以P(ξ=0)= =
=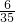 ;
;
ξ=2表示恰有两个区域用红色鲜花”,
当区域A、D同色时,共有5×4×3×1×3=180种;
当区域A、D不同色时,共有5×4×3×2×2=240种;
∴所有基本事件总数为:180+240=420种
又因为A、D为红色时,共有4×3×3=36种;
B、E为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种
所以恰有两个区域用红色鲜花的概率P(ξ=2)=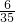 ;
;
所以P(ξ=1)=1-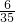 -
-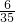 =
= .
.
E(ξ)=0×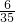 +1×
+1× +2×
+2×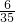 =1.
=1.
故答案为:1
点评:本题考查离散型随机变量的期望,解题的关键是熟练利用排列与组合的知识对区域进行正确的涂色,与离散型随机变量的期望公式,本题是一个中档题目.
分析:由题意知花圃中红色鲜花区域的块数可能为0,1,2,当ξ=0时,表示用黄、蓝、白、橙四种颜色来涂色,ξ=2表示恰有两个区域用红色鲜花”,求出相应的概率即可求得期望.
解答:由题意可得随机变量ξ的取值分别为0,1,2.
则当ξ=0时,表示用黄、蓝、白、橙四种颜色来涂色,
若A、D为同色时,共有4×3×2×1×2=48种;
若A、D为不同色时,共有4×3×2×1×1=24种;
即ξ=0所包含的基本事件有48+24=72种,
所以P(ξ=0)=
 =
=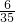 ;
;ξ=2表示恰有两个区域用红色鲜花”,
当区域A、D同色时,共有5×4×3×1×3=180种;
当区域A、D不同色时,共有5×4×3×2×2=240种;
∴所有基本事件总数为:180+240=420种
又因为A、D为红色时,共有4×3×3=36种;
B、E为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种
所以恰有两个区域用红色鲜花的概率P(ξ=2)=
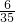 ;
;所以P(ξ=1)=1-
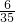 -
-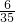 =
= .
.E(ξ)=0×
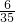 +1×
+1× +2×
+2×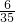 =1.
=1.故答案为:1
点评:本题考查离散型随机变量的期望,解题的关键是熟练利用排列与组合的知识对区域进行正确的涂色,与离散型随机变量的期望公式,本题是一个中档题目.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
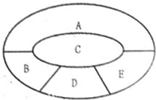 如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择. (2011•邢台一模)如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(2011•邢台一模)如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.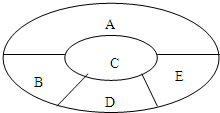 如图,某学校要用鲜花布置花圃中A,B,C,D,E五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同的颜色的鲜花,现有红,黄,蓝,白,紫五种不同颜色的鲜花可供任意选择,记X表示花圃中用红色鲜花布置的区域的个数,则随机变量X的期望EX=
如图,某学校要用鲜花布置花圃中A,B,C,D,E五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同的颜色的鲜花,现有红,黄,蓝,白,紫五种不同颜色的鲜花可供任意选择,记X表示花圃中用红色鲜花布置的区域的个数,则随机变量X的期望EX=