题目内容
已知函数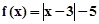 ,
,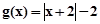 。
。
(1)求不等式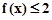 的解集;
的解集;
(2)若不等式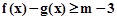 有解,求实数
有解,求实数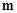 的取值范围。
的取值范围。
(1) ;(2)
;(2) .
.
解析试题分析:(1)根据绝对值的几何意义去掉绝对值, ,解出
,解出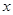 ;此问的关键是利用公式去掉绝对值,解不等式.
;此问的关键是利用公式去掉绝对值,解不等式.
(2)转化为 有解的问题,利用绝对值的性质,
有解的问题,利用绝对值的性质, 求出
求出 的范围,因为是有解,所以
的范围,因为是有解,所以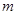 小于其最大值,即可求出范围,此问的关键是利用不等式的性质找到左边含绝对值的式子的范围.
小于其最大值,即可求出范围,此问的关键是利用不等式的性质找到左边含绝对值的式子的范围.
试题解析:(1)由题意得 ,得
,得
∴
所以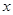 的取值范围是
的取值范围是 。 5分
。 5分
(2)因为 有解
有解
所以 有解
有解
∴
所以 ,即
,即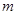 的取值范围是
的取值范围是 。 10分
。 10分
考点:1.解绝对值的不等式;2.绝对值的性质.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
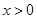 ,
,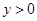 ,
,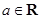 ,
,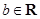 .求证
.求证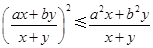 .
. (2-
(2- ≥
≥ .
. +
+ ≥2.
≥2. +lg
+lg +lg
+lg >lga+lgb+lgc.
>lga+lgb+lgc. +
+ +
+ ≥5.
≥5. +
+ 的最小值.
的最小值. ≤
≤ +
+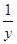 +xy;
+xy;
 ;
;
 与
与 的大小.
的大小.