Question

已知y=f（x）的反函数是y=f^-1（x），若方程f（x）+x-1=0与f^-1（x）+x-1=0的实数解分别为α，β，则α+β=（　　）

A．1

B．2

C．-1

D．-2

Answer 1

方程f（x）+x-1=0化成：f（x）=1-x，
f^-1（x）+x-1=0化成：f^-1（x）=1-x，
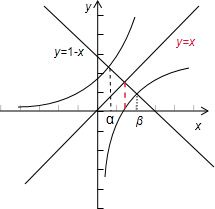
分别画出函数y=f（x），y=f^-1（x），y=1-x的图象，如图．
原方程的根看成是图象的交点的横坐标，
由于函数y=f（x），y=f^-1（x）的图关于直线 y=x对称，
∴α，β的中点的横坐标是直线y=x与y=1-x交点的横坐标，
直线y=x与y=1-x交点的横坐标是：

1

2

由中点坐标公式得：α+β=1．
故选A．