题目内容
设A,B,C是半径为1的圆上三点,若AB=
,则
•
的最大值为( )
| 3 |
| AB |
| AC |
分析:先根据余弦定义可求出AB边所对的圆心角,从而得到角C,然后根据数量积公式将
•
转化成角B的三角函数,从而可求出最值.
| AB |
| AC |
解答:解:∵A,B,C是半径为1的圆上三点,AB=
,
∴根据余弦定理可知AB边所对的圆心角为120°则∠C=60°
根据正弦定理可知AC=2sinB
∴
•
=
×2sinBcos(120°-B)=2
sinB(-
cosB+
sinB)
=-
sinBcosB+3sin2B
=-
sin2B+
(1-cos2B)
=
-
sin(2B+60°)
当B=60°时
•
取最大值为
+
故选B.
| 3 |
∴根据余弦定理可知AB边所对的圆心角为120°则∠C=60°
根据正弦定理可知AC=2sinB
∴
| AB |
| AC |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=-
| 3 |
=-
| ||
| 2 |
| 3 |
| 2 |
=
| 3 |
| 2 |
| 3 |
当B=60°时
| AB |
| AC |
| 3 |
| 2 |
| 3 |
故选B.
点评:本题主要考查了向量在几何中的应用,以及余弦定理和正弦定理的应用,同时考查了三角函数的值域,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.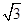
 ,则
,则 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为 ,O为球心,
,O为球心,